sierpinski_foam2

The sierpinski gasket is a classic example of a fractal image with self-similar properties across all length scales. It has also been extensively analyzed so these properties are well know. The sierpinski_foam2 is a 3D version of the gasket.

import porespy as ps
import matplotlib.pyplot as plt
import numpy as np
import inspect
inspect.signature(ps.generators.sierpinski_foam2)

<Signature (shape, n=5)>

shape

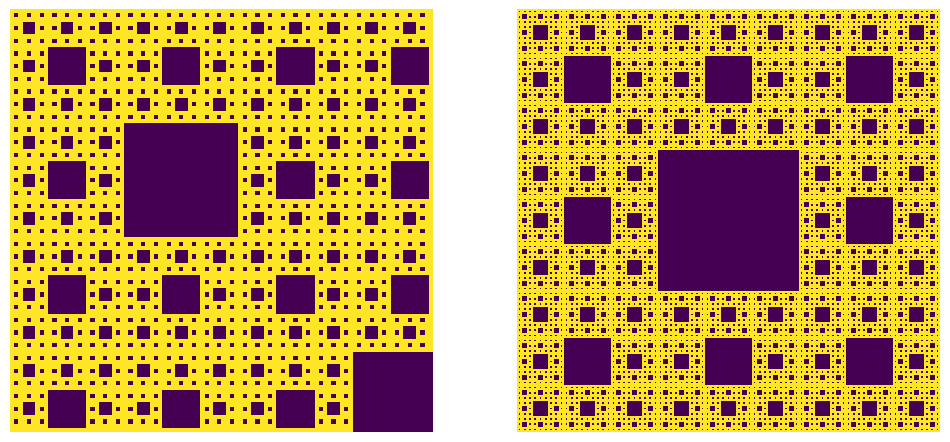
The original version of this generator did not accept shape, and instead its size was dictated by the number of divisions requested. The new version does except shape and instead it truncates the pattern if the requested number of divisions exceeds the shape.

In the images below, the image of size 100 by 100 is not symmetrical. If the full pattern is desired, then the shape must be set to 3**n in all directions, as shown on the right (n=5 is the default value).

fig, ax = plt.subplots(1, 2, figsize=[12, 6])

im = ps.generators.sierpinski_foam2(shape=[100, 100])
ax[0].imshow(im, interpolation='none')
ax[0].axis(False)

im = ps.generators.sierpinski_foam2(shape=[3**5, 3**5])
ax[1].imshow(im, interpolation='none')
ax[1].axis(False);

n

The number of times the patter is divided is controlled by the n parameter:

fig, ax = plt.subplots(1, 2, figsize=[12, 6])

n = 3
im = ps.generators.sierpinski_foam2(shape=[3**n, 3**n])
ax[0].imshow(im, interpolation='none')
ax[0].axis(False)

n = 4
im = ps.generators.sierpinski_foam2(shape=[3**n, 3**n])
ax[1].imshow(im, interpolation='none')
ax[1].axis(False);