Generating Sphere Packings from Digital Rocks Portal¶
The digital rocks portal is a great resource for finding a variety of tomographic images. However, several of the items that can be found there are actually CSV files containing the coordinates and radii of spheres in a packing. In this tutorial we’ll look at a few of these and see how the spheres_from_coords function handles them.
import porespy as ps
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
[01:02:41] ERROR PARDISO solver not installed, run `pip install pypardiso`. Otherwise, _workspace.py:56 simulations will be slow. Apple M chips not supported.
Finney Packing¶
The first one we’ll look at is the Finney Packing.
To start with, we’ll download the file and place it in the same directory as this notebook, which makes it easier to open. We’ll then use pandas to read the file, which always does an excellent job reading CSV files.
df = pd.read_csv('finney_packing.csv')
print(df)
ID X Y Z
0 1 -0.324554 0.081522 -0.452144
1 2 0.139446 -1.232478 0.985858
2 3 1.641446 -0.078478 -0.876144
3 4 -1.182554 0.557522 1.385856
4 5 1.713446 0.143522 1.107856
... ... ... ... ...
4016 4017 3.547448 11.858320 13.735856
4017 4018 5.597446 4.971524 -16.908144
4018 4019 -8.748554 16.023504 2.961856
4019 4020 7.353446 -16.964479 -0.500142
4020 4021 -13.228554 7.943524 10.203858
[4021 rows x 4 columns]
We can see that this file has coordinates for 4021 spheres in 3-dimensions, though no units are given. It also does not include any information about the radii of the spheres. In fact, Prof. Finney has left us the following challenge:
“With some effort, sphere locations can be used to produce a volumetric image at any resolution you need.”
Challenge accepted…
We’ll start by assuming that the coordinates are in units of “sphere radii”, so if we want spheres with a radii of 10 voxels, we need to (a) scale all the X, Y, and Z values by 10, and (b) insert a column into the DataFrame for “R”, with all values equal to 10.
df['X'] *= 10
df['Y'] *= 10
df['Z'] *= 10
df['R'] = 10.0
im = ps.generators.spheres_from_coords(df)
Let’s see how it looks using a couple of the quick visualization functions in PoreSpy:
fig, ax = plt.subplots(1, 2, figsize=[16, 8])
ax[0].imshow(ps.visualization.sem(~im), cmap=plt.cm.twilight_shifted)
ax[1].imshow(ps.visualization.show_planes(im));
That was easy!
Justing kidding, it took ages to write the spheres_from_coords function to handle all the edge cases, such as the negative numbers in the “finney_packing.csv” file.
Bidisperse Sphere Packs¶
Next we’ll look at the bidisperse sphere packs posted by Bihani and Daigle. This one is a bit more challenging because the spheres are different size, but the spheres_from_coords function should be able to handle this too:
df = pd.read_csv("5to1_VL49.9_2.csv")
print(df)
3.0182 0.8832 9.5101 0.5
0 5.16800 7.4590 9.91010 0.1
1 3.52470 6.0797 9.91050 0.1
2 9.77820 9.9506 9.91000 0.1
3 3.66130 3.3672 9.91040 0.1
4 1.25630 3.7398 9.91020 0.1
... ... ... ... ...
78539 3.00070 9.0727 0.83122 0.1
78540 7.81650 8.9274 0.59451 0.1
78541 4.27500 6.6440 0.83542 0.1
78542 0.93797 1.4616 0.81609 0.1
78543 5.73430 3.9447 1.08350 0.1
[78544 rows x 4 columns]
The first thing to notice is that the CSV file was not formatted as expected, as it lacked a header row so took the first row of data as the header. We can alter the read_csv function to account for this. The docstring for this functin is ridiculously long, but that is the price to pay for such a flexible function. After some digging we can learn that it’s possible to not read a header from the file, and to supply our own column names:
df = pd.read_csv("5to1_VL49.9_2.csv", header=None, names=['X', 'Y', 'Z', 'R'])
print(df)
X Y Z R
0 3.01820 0.8832 9.51010 0.5
1 5.16800 7.4590 9.91010 0.1
2 3.52470 6.0797 9.91050 0.1
3 9.77820 9.9506 9.91000 0.1
4 3.66130 3.3672 9.91040 0.1
... ... ... ... ...
78540 3.00070 9.0727 0.83122 0.1
78541 7.81650 8.9274 0.59451 0.1
78542 4.27500 6.6440 0.83542 0.1
78543 0.93797 1.4616 0.81609 0.1
78544 5.73430 3.9447 1.08350 0.1
[78545 rows x 4 columns]
Like the previous packing, we need to scale the coordinates and radii. We don’t want this file to become too large, so let’s go with 25 voxels for the largest spheres and 5 voxels for the smaller ones. This means scaling by 50x.
df['X'] *= 50
df['Y'] *= 50
df['Z'] *= 50
df['R'] *= 50
print(df)
X Y Z R
0 150.9100 44.160 475.5050 25.0
1 258.4000 372.950 495.5050 5.0
2 176.2350 303.985 495.5250 5.0
3 488.9100 497.530 495.5000 5.0
4 183.0650 168.360 495.5200 5.0
... ... ... ... ...
78540 150.0350 453.635 41.5610 5.0
78541 390.8250 446.370 29.7255 5.0
78542 213.7500 332.200 41.7710 5.0
78543 46.8985 73.080 40.8045 5.0
78544 286.7150 197.235 54.1750 5.0
[78545 rows x 4 columns]
Before proceeding, let’s estimate how large this image will be:
(df['X'].max()*df['Y'].max()*df['Z'].max())**0.333
np.float64(495.4219546770277)
A 500-cubed image is fairly manageble, but care should be taken not to get too aggressive with high resolutions. Probably trial-and-error is the best approach, starting with small values and increasing until you’re satisfied with result AND willing to wait the required time. A 500-cubed image should only take 5-10 seconds, but this number grows quickly as the image size increase and the size of the spheres being inserted increases
im = ps.generators.spheres_from_coords(df)
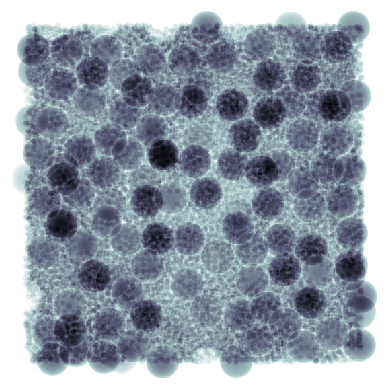
This image is difficult to visualize in 2D due to the small spheres essentially filling much of the image. The following is a fake x-ray attenuation image through the last 100 layers in the z-direction. The large spheres and densely packed fines are both visible.
fig, ax = plt.subplots()
ax.imshow(ps.visualization.xray(~im[..., :100], axis=2), interpolation='none', origin='lower', cmap=plt.cm.bone)
ax.axis(False);
