Using AI based diffusive size factors for extracted networks#
This notebook illustrates the use of the deep learning based diffusive conductance algorithm decribed here. PoreSpy’s diffusive_size_factor_AI includes the steps for predicting the diffusive size factors of the conduit images. Note that the diffusive conductance of the conduits can be then calculated by multiplying the size factor by diffusivity of the phase. The function takes in the images of segmented porous medium and returns an array of diffusive size factors for all conduits in the image. Therefore, the framework can be applied to both one conduit image as well as a segmented image of porous medium:
Trained model and supplementary materials#
To use the diffusive_size_factor_AI, the trained model, and training data distribution are required. The AI model files and additional files used in this example are available here. The folder contains following files:
Trained model weights: This file includes only weights of the deep learning layers. To use this file, the Resnet50 model structure must be built first.
Trained data distribution: This file will be used in denormalizing predicted values based on normalized transform applied on training data. The denormalizing step is included in
diffusive_size_factor_AImethod.Finite difference diffusive conductance: This file is used in this example to compare the prediction results with finite difference method for segmented regions. Note: Finite difference-based size factors can be calculated using PoreSpy’s
diffusive_size_factor_DNSmethod.
Let’s download the tensorflow files required to run this notebook:
try:
import tensorflow as tf
except ImportError:
!pip install tensorflow
try:
import sklearn
except ImportError:
!pip install scikit-learn
import os
if not os.path.exists("sf-model-lib"):
!git clone https://github.com/PMEAL/sf-model-lib
Collecting tensorflow
Obtaining dependency information for tensorflow from https://files.pythonhosted.org/packages/88/cc/14affad82a28640974ff2a37c177269a0a088266104ddf76a01eac21c9ac/tensorflow-2.13.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata
Downloading tensorflow-2.13.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata (3.4 kB)
Collecting absl-py>=1.0.0 (from tensorflow)
Downloading absl_py-1.4.0-py3-none-any.whl (126 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/126.5 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━ 61.4/126.5 kB 2.0 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 126.5/126.5 kB 2.3 MB/s eta 0:00:00
?25h
Collecting astunparse>=1.6.0 (from tensorflow)
Downloading astunparse-1.6.3-py2.py3-none-any.whl (12 kB)
Collecting flatbuffers>=23.1.21 (from tensorflow)
Obtaining dependency information for flatbuffers>=23.1.21 from https://files.pythonhosted.org/packages/6f/12/d5c79ee252793ffe845d58a913197bfa02ae9a0b5c9bc3dc4b58d477b9e7/flatbuffers-23.5.26-py2.py3-none-any.whl.metadata
Downloading flatbuffers-23.5.26-py2.py3-none-any.whl.metadata (850 bytes)
Collecting gast<=0.4.0,>=0.2.1 (from tensorflow)
Downloading gast-0.4.0-py3-none-any.whl (9.8 kB)
Collecting google-pasta>=0.1.1 (from tensorflow)
Downloading google_pasta-0.2.0-py3-none-any.whl (57 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/57.5 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 57.5/57.5 kB 13.5 MB/s eta 0:00:00
?25h
Collecting grpcio<2.0,>=1.24.3 (from tensorflow)
Obtaining dependency information for grpcio<2.0,>=1.24.3 from https://files.pythonhosted.org/packages/29/f7/32768339888afbd04ce81121d00cc171a84cff3cb9be135e7c3b9c5836b9/grpcio-1.58.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata
Downloading grpcio-1.58.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata (4.0 kB)
Requirement already satisfied: h5py>=2.9.0 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from tensorflow) (3.9.0)
Collecting keras<2.14,>=2.13.1 (from tensorflow)
Obtaining dependency information for keras<2.14,>=2.13.1 from https://files.pythonhosted.org/packages/2e/f3/19da7511b45e80216cbbd9467137b2d28919c58ba1ccb971435cb631e470/keras-2.13.1-py3-none-any.whl.metadata
Downloading keras-2.13.1-py3-none-any.whl.metadata (2.4 kB)
Collecting libclang>=13.0.0 (from tensorflow)
Obtaining dependency information for libclang>=13.0.0 from https://files.pythonhosted.org/packages/ea/df/55525e489c43f9dbb6c8ea27d8a567b3dcd18a22f3c45483055f5ca6611d/libclang-16.0.6-py2.py3-none-manylinux2010_x86_64.whl.metadata
Downloading libclang-16.0.6-py2.py3-none-manylinux2010_x86_64.whl.metadata (5.2 kB)
Collecting numpy<=1.24.3,>=1.22 (from tensorflow)
Downloading numpy-1.24.3-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (17.3 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/17.3 MB ? eta -:--:--
━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 3.1/17.3 MB 87.0 MB/s eta 0:00:01
━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━ 6.5/17.3 MB 92.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━ 9.9/17.3 MB 92.2 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━ 13.2/17.3 MB 93.9 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━ 16.5/17.3 MB 94.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 17.3/17.3 MB 95.7 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 17.3/17.3 MB 95.7 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 17.3/17.3 MB 55.8 MB/s eta 0:00:00
?25h
Collecting opt-einsum>=2.3.2 (from tensorflow)
Downloading opt_einsum-3.3.0-py3-none-any.whl (65 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/65.5 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 65.5/65.5 kB 15.2 MB/s eta 0:00:00
?25hRequirement already satisfied: packaging in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from tensorflow) (23.1)
Collecting protobuf!=4.21.0,!=4.21.1,!=4.21.2,!=4.21.3,!=4.21.4,!=4.21.5,<5.0.0dev,>=3.20.3 (from tensorflow)
Obtaining dependency information for protobuf!=4.21.0,!=4.21.1,!=4.21.2,!=4.21.3,!=4.21.4,!=4.21.5,<5.0.0dev,>=3.20.3 from https://files.pythonhosted.org/packages/bb/c3/6a06208ecf0934ecaf509b51c52a6cf688586f54ae81ac65c56124571494/protobuf-4.24.3-cp37-abi3-manylinux2014_x86_64.whl.metadata
Downloading protobuf-4.24.3-cp37-abi3-manylinux2014_x86_64.whl.metadata (540 bytes)
Requirement already satisfied: setuptools in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from tensorflow) (56.0.0)
Requirement already satisfied: six>=1.12.0 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from tensorflow) (1.16.0)
Collecting tensorboard<2.14,>=2.13 (from tensorflow)
Downloading tensorboard-2.13.0-py3-none-any.whl (5.6 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/5.6 MB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━ 4.2/5.6 MB 107.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 5.6/5.6 MB 97.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 5.6/5.6 MB 67.0 MB/s eta 0:00:00
?25h
Collecting tensorflow-estimator<2.14,>=2.13.0 (from tensorflow)
Obtaining dependency information for tensorflow-estimator<2.14,>=2.13.0 from https://files.pythonhosted.org/packages/72/5c/c318268d96791c6222ad7df1651bbd1b2409139afeb6f468c0f327177016/tensorflow_estimator-2.13.0-py2.py3-none-any.whl.metadata
Downloading tensorflow_estimator-2.13.0-py2.py3-none-any.whl.metadata (1.3 kB)
Collecting termcolor>=1.1.0 (from tensorflow)
Downloading termcolor-2.3.0-py3-none-any.whl (6.9 kB)
Collecting typing-extensions<4.6.0,>=3.6.6 (from tensorflow)
Downloading typing_extensions-4.5.0-py3-none-any.whl (27 kB)
Requirement already satisfied: wrapt>=1.11.0 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from tensorflow) (1.15.0)
Collecting tensorflow-io-gcs-filesystem>=0.23.1 (from tensorflow)
Obtaining dependency information for tensorflow-io-gcs-filesystem>=0.23.1 from https://files.pythonhosted.org/packages/25/f6/0f259f41abaa489f185e16d397d5f5a5973970d4677c7d39456cea6f4453/tensorflow_io_gcs_filesystem-0.34.0-cp38-cp38-manylinux_2_12_x86_64.manylinux2010_x86_64.whl.metadata
Downloading tensorflow_io_gcs_filesystem-0.34.0-cp38-cp38-manylinux_2_12_x86_64.manylinux2010_x86_64.whl.metadata (14 kB)
Collecting wheel<1.0,>=0.23.0 (from astunparse>=1.6.0->tensorflow)
Obtaining dependency information for wheel<1.0,>=0.23.0 from https://files.pythonhosted.org/packages/b8/8b/31273bf66016be6ad22bb7345c37ff350276cfd46e389a0c2ac5da9d9073/wheel-0.41.2-py3-none-any.whl.metadata
Using cached wheel-0.41.2-py3-none-any.whl.metadata (2.2 kB)
Collecting google-auth<3,>=1.6.3 (from tensorboard<2.14,>=2.13->tensorflow)
Obtaining dependency information for google-auth<3,>=1.6.3 from https://files.pythonhosted.org/packages/9d/44/5a992cb9d7bf8aaae73bc5adaf721ad08731c9d00c1c17999a8691404b0c/google_auth-2.23.0-py2.py3-none-any.whl.metadata
Downloading google_auth-2.23.0-py2.py3-none-any.whl.metadata (4.2 kB)
Collecting google-auth-oauthlib<1.1,>=0.5 (from tensorboard<2.14,>=2.13->tensorflow)
Downloading google_auth_oauthlib-1.0.0-py2.py3-none-any.whl (18 kB)
Collecting markdown>=2.6.8 (from tensorboard<2.14,>=2.13->tensorflow)
Obtaining dependency information for markdown>=2.6.8 from https://files.pythonhosted.org/packages/1a/b5/228c1cdcfe138f1a8e01ab1b54284c8b83735476cb22b6ba251656ed13ad/Markdown-3.4.4-py3-none-any.whl.metadata
Downloading Markdown-3.4.4-py3-none-any.whl.metadata (6.9 kB)
Requirement already satisfied: requests<3,>=2.21.0 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from tensorboard<2.14,>=2.13->tensorflow) (2.31.0)
Collecting tensorboard-data-server<0.8.0,>=0.7.0 (from tensorboard<2.14,>=2.13->tensorflow)
Obtaining dependency information for tensorboard-data-server<0.8.0,>=0.7.0 from https://files.pythonhosted.org/packages/02/52/fb9e51fba47951aabd7a6b25e41d73eae94208ccf62d886168096941a781/tensorboard_data_server-0.7.1-py3-none-manylinux2014_x86_64.whl.metadata
Downloading tensorboard_data_server-0.7.1-py3-none-manylinux2014_x86_64.whl.metadata (1.1 kB)
Collecting werkzeug>=1.0.1 (from tensorboard<2.14,>=2.13->tensorflow)
Obtaining dependency information for werkzeug>=1.0.1 from https://files.pythonhosted.org/packages/9b/59/a7c32e3d8d0e546a206e0552a2c04444544f15c1da4a01df8938d20c6ffc/werkzeug-2.3.7-py3-none-any.whl.metadata
Downloading werkzeug-2.3.7-py3-none-any.whl.metadata (4.1 kB)
Collecting cachetools<6.0,>=2.0.0 (from google-auth<3,>=1.6.3->tensorboard<2.14,>=2.13->tensorflow)
Obtaining dependency information for cachetools<6.0,>=2.0.0 from https://files.pythonhosted.org/packages/a9/c9/c8a7710f2cedcb1db9224fdd4d8307c9e48cbddc46c18b515fefc0f1abbe/cachetools-5.3.1-py3-none-any.whl.metadata
Downloading cachetools-5.3.1-py3-none-any.whl.metadata (5.2 kB)
Collecting pyasn1-modules>=0.2.1 (from google-auth<3,>=1.6.3->tensorboard<2.14,>=2.13->tensorflow)
Downloading pyasn1_modules-0.3.0-py2.py3-none-any.whl (181 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/181.3 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 181.3/181.3 kB 32.4 MB/s eta 0:00:00
?25h
Collecting rsa<5,>=3.1.4 (from google-auth<3,>=1.6.3->tensorboard<2.14,>=2.13->tensorflow)
Downloading rsa-4.9-py3-none-any.whl (34 kB)
Collecting urllib3<2.0 (from google-auth<3,>=1.6.3->tensorboard<2.14,>=2.13->tensorflow)
Obtaining dependency information for urllib3<2.0 from https://files.pythonhosted.org/packages/c5/05/c214b32d21c0b465506f95c4f28ccbcba15022e000b043b72b3df7728471/urllib3-1.26.16-py2.py3-none-any.whl.metadata
Downloading urllib3-1.26.16-py2.py3-none-any.whl.metadata (48 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/48.4 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 48.4/48.4 kB 11.4 MB/s eta 0:00:00
?25h
Collecting requests-oauthlib>=0.7.0 (from google-auth-oauthlib<1.1,>=0.5->tensorboard<2.14,>=2.13->tensorflow)
Downloading requests_oauthlib-1.3.1-py2.py3-none-any.whl (23 kB)
Requirement already satisfied: importlib-metadata>=4.4 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from markdown>=2.6.8->tensorboard<2.14,>=2.13->tensorflow) (6.8.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from requests<3,>=2.21.0->tensorboard<2.14,>=2.13->tensorflow) (3.2.0)
Requirement already satisfied: idna<4,>=2.5 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from requests<3,>=2.21.0->tensorboard<2.14,>=2.13->tensorflow) (3.4)
Requirement already satisfied: certifi>=2017.4.17 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from requests<3,>=2.21.0->tensorboard<2.14,>=2.13->tensorflow) (2023.7.22)
Requirement already satisfied: MarkupSafe>=2.1.1 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from werkzeug>=1.0.1->tensorboard<2.14,>=2.13->tensorflow) (2.1.3)
Requirement already satisfied: zipp>=0.5 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from importlib-metadata>=4.4->markdown>=2.6.8->tensorboard<2.14,>=2.13->tensorflow) (3.16.2)
Collecting pyasn1<0.6.0,>=0.4.6 (from pyasn1-modules>=0.2.1->google-auth<3,>=1.6.3->tensorboard<2.14,>=2.13->tensorflow)
Downloading pyasn1-0.5.0-py2.py3-none-any.whl (83 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/83.9 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 83.9/83.9 kB 17.6 MB/s eta 0:00:00
?25h
Collecting oauthlib>=3.0.0 (from requests-oauthlib>=0.7.0->google-auth-oauthlib<1.1,>=0.5->tensorboard<2.14,>=2.13->tensorflow)
Downloading oauthlib-3.2.2-py3-none-any.whl (151 kB)
?25l
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/151.7 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 151.7/151.7 kB 28.6 MB/s eta 0:00:00
?25h
Downloading tensorflow-2.13.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (524.1 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/524.1 MB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 4.2/524.1 MB 105.3 MB/s eta 0:00:05
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 6.3/524.1 MB 81.3 MB/s eta 0:00:07
╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 9.4/524.1 MB 82.4 MB/s eta 0:00:07
╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 12.3/524.1 MB 79.0 MB/s eta 0:00:07
━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 15.4/524.1 MB 78.8 MB/s eta 0:00:07
━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 16.8/524.1 MB 83.1 MB/s eta 0:00:07
━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 16.8/524.1 MB 83.1 MB/s eta 0:00:07
━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 16.8/524.1 MB 83.1 MB/s eta 0:00:07
━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 20.3/524.1 MB 47.9 MB/s eta 0:00:11
━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 22.0/524.1 MB 48.6 MB/s eta 0:00:11
━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 24.5/524.1 MB 43.5 MB/s eta 0:00:12
━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 27.7/524.1 MB 77.6 MB/s eta 0:00:07
━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 31.2/524.1 MB 75.6 MB/s eta 0:00:07
━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 34.5/524.1 MB 92.8 MB/s eta 0:00:06
━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 38.1/524.1 MB 98.5 MB/s eta 0:00:05
━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 41.7/524.1 MB 99.7 MB/s eta 0:00:05
━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 45.3/524.1 MB 101.1 MB/s eta 0:00:05
━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 48.8/524.1 MB 101.7 MB/s eta 0:00:05
━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 52.5/524.1 MB 101.4 MB/s eta 0:00:05
━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 56.2/524.1 MB 101.0 MB/s eta 0:00:05
━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 59.0/524.1 MB 96.4 MB/s eta 0:00:05
━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 62.7/524.1 MB 93.5 MB/s eta 0:00:05
━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 66.2/524.1 MB 93.3 MB/s eta 0:00:05
━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 69.7/524.1 MB 100.9 MB/s eta 0:00:05
━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 73.6/524.1 MB 104.5 MB/s eta 0:00:05
━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 76.5/524.1 MB 105.5 MB/s eta 0:00:05
━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 76.5/524.1 MB 105.5 MB/s eta 0:00:05
━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 79.1/524.1 MB 68.5 MB/s eta 0:00:07
━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 82.3/524.1 MB 65.0 MB/s eta 0:00:07
━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 85.2/524.1 MB 61.6 MB/s eta 0:00:08
━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 88.2/524.1 MB 83.2 MB/s eta 0:00:06
━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 91.4/524.1 MB 84.5 MB/s eta 0:00:06
━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 94.3/524.1 MB 83.0 MB/s eta 0:00:06
━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 98.1/524.1 MB 91.0 MB/s eta 0:00:05
━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 102.3/524.1 MB 102.1 MB/s eta 0:00:05
━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 106.0/524.1 MB 105.9 MB/s eta 0:00:04
━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 109.9/524.1 MB 104.9 MB/s eta 0:00:04
━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 113.9/524.1 MB 107.3 MB/s eta 0:00:04
━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 117.2/524.1 MB 104.4 MB/s eta 0:00:04
━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 120.9/524.1 MB 102.3 MB/s eta 0:00:04
━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 124.9/524.1 MB 102.1 MB/s eta 0:00:04
━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 127.6/524.1 MB 105.6 MB/s eta 0:00:04
━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 131.0/524.1 MB 92.0 MB/s eta 0:00:05
━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 134.2/524.1 MB 84.6 MB/s eta 0:00:05
━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 136.7/524.1 MB 76.9 MB/s eta 0:00:06
━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 139.3/524.1 MB 76.9 MB/s eta 0:00:06
━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 141.3/524.1 MB 71.7 MB/s eta 0:00:06
━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 144.1/524.1 MB 67.8 MB/s eta 0:00:06
━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 147.9/524.1 MB 74.6 MB/s eta 0:00:06
━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 151.7/524.1 MB 99.2 MB/s eta 0:00:04
━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━ 155.4/524.1 MB 107.6 MB/s eta 0:00:04
━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━ 159.3/524.1 MB 107.1 MB/s eta 0:00:04
━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━ 163.2/524.1 MB 107.7 MB/s eta 0:00:04
━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━ 166.8/524.1 MB 107.6 MB/s eta 0:00:04
━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━ 170.6/524.1 MB 106.0 MB/s eta 0:00:04
━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━ 174.3/524.1 MB 104.1 MB/s eta 0:00:04
━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━ 178.1/524.1 MB 106.4 MB/s eta 0:00:04
━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━ 180.9/524.1 MB 95.1 MB/s eta 0:00:04
━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━ 183.9/524.1 MB 87.6 MB/s eta 0:00:04
━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━ 187.6/524.1 MB 86.6 MB/s eta 0:00:04
━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━ 191.1/524.1 MB 93.4 MB/s eta 0:00:04
━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━ 194.5/524.1 MB 101.0 MB/s eta 0:00:04
━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━ 198.1/524.1 MB 100.3 MB/s eta 0:00:04
━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━ 201.5/524.1 MB 98.6 MB/s eta 0:00:04
━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━ 204.9/524.1 MB 98.5 MB/s eta 0:00:04
━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━ 208.5/524.1 MB 99.5 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━ 210.2/524.1 MB 82.5 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━ 212.2/524.1 MB 73.7 MB/s eta 0:00:05
━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━ 216.0/524.1 MB 75.7 MB/s eta 0:00:05
━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━ 219.8/524.1 MB 76.5 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━ 223.4/524.1 MB 103.0 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━ 227.2/524.1 MB 105.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━ 230.6/524.1 MB 101.4 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━ 234.3/524.1 MB 101.6 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━ 237.9/524.1 MB 101.8 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━ 241.2/524.1 MB 100.0 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━ 244.7/524.1 MB 98.5 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━ 247.7/524.1 MB 91.4 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━ 250.0/524.1 MB 83.4 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━━ 253.5/524.1 MB 82.9 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━ 257.0/524.1 MB 84.4 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━ 260.2/524.1 MB 93.7 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━ 263.0/524.1 MB 87.4 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━━ 266.1/524.1 MB 84.3 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━ 269.1/524.1 MB 83.2 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━ 272.3/524.1 MB 81.7 MB/s eta 0:00:04
━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━ 275.5/524.1 MB 89.7 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━ 278.9/524.1 MB 88.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━━ 281.6/524.1 MB 86.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━ 284.8/524.1 MB 83.3 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━ 287.5/524.1 MB 82.5 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━ 290.9/524.1 MB 83.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━━ 293.6/524.1 MB 82.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━ 297.0/524.1 MB 89.0 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━ 299.5/524.1 MB 81.5 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━ 302.3/524.1 MB 78.4 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━━ 305.3/524.1 MB 78.2 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━ 308.4/524.1 MB 78.0 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━ 311.3/524.1 MB 85.5 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━ 314.5/524.1 MB 84.5 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━ 317.5/524.1 MB 83.0 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━━ 320.8/524.1 MB 88.1 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━ 323.9/524.1 MB 86.1 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━ 326.8/524.1 MB 85.8 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━ 330.1/524.1 MB 88.0 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━━ 332.6/524.1 MB 80.8 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━ 335.6/524.1 MB 83.2 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━ 339.1/524.1 MB 85.4 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━ 342.3/524.1 MB 86.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━━ 345.1/524.1 MB 86.2 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━ 348.2/524.1 MB 85.3 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━ 351.5/524.1 MB 85.6 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━ 354.6/524.1 MB 83.5 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━━ 357.5/524.1 MB 87.5 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━ 360.7/524.1 MB 83.0 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━ 364.2/524.1 MB 86.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━ 367.7/524.1 MB 90.4 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━ 369.0/524.1 MB 88.0 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━ 371.8/524.1 MB 73.6 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━ 374.2/524.1 MB 66.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━ 377.2/524.1 MB 63.9 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━ 379.8/524.1 MB 76.7 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━ 382.0/524.1 MB 70.3 MB/s eta 0:00:03
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━ 385.0/524.1 MB 76.9 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━ 388.3/524.1 MB 82.5 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━ 391.7/524.1 MB 81.5 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━ 394.9/524.1 MB 90.7 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━ 398.3/524.1 MB 92.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━ 401.6/524.1 MB 92.8 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━ 404.1/524.1 MB 85.8 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 407.6/524.1 MB 86.4 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 410.0/524.1 MB 81.8 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━ 411.7/524.1 MB 78.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━ 412.7/524.1 MB 14.4 MB/s eta 0:00:08
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━ 415.8/524.1 MB 14.3 MB/s eta 0:00:08
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━ 418.6/524.1 MB 14.2 MB/s eta 0:00:08
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━ 421.3/524.1 MB 14.2 MB/s eta 0:00:08
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━ 424.1/524.1 MB 78.2 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━ 427.0/524.1 MB 79.3 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━ 429.5/524.1 MB 77.7 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━ 432.1/524.1 MB 75.4 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━ 435.5/524.1 MB 80.5 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━ 438.2/524.1 MB 78.2 MB/s eta 0:00:02
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━ 441.5/524.1 MB 89.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━ 444.8/524.1 MB 86.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━ 447.4/524.1 MB 84.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━ 449.8/524.1 MB 79.9 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━ 453.3/524.1 MB 81.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━ 456.7/524.1 MB 84.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━ 459.7/524.1 MB 85.2 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━ 462.8/524.1 MB 89.2 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━ 465.8/524.1 MB 84.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━ 468.7/524.1 MB 83.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━ 471.3/524.1 MB 81.2 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━ 474.6/524.1 MB 83.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━ 478.1/524.1 MB 87.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━ 481.2/524.1 MB 85.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━ 484.1/524.1 MB 89.0 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━ 487.0/524.1 MB 84.2 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━ 489.4/524.1 MB 77.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━ 493.0/524.1 MB 80.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━ 496.7/524.1 MB 88.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━ 500.3/524.1 MB 101.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━ 503.4/524.1 MB 98.7 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━ 504.7/524.1 MB 80.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━ 507.7/524.1 MB 72.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━ 510.2/524.1 MB 65.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺ 512.8/524.1 MB 63.5 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺ 515.9/524.1 MB 76.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 518.7/524.1 MB 76.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 521.6/524.1 MB 80.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 524.1/524.1 MB 83.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 524.1/524.1 MB 2.4 MB/s eta 0:00:00
?25hDownloading flatbuffers-23.5.26-py2.py3-none-any.whl (26 kB)
Downloading grpcio-1.58.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (5.3 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/5.3 MB ? eta -:--:--
━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.4/5.3 MB 42.7 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━ 3.9/5.3 MB 56.9 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 5.3/5.3 MB 63.0 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 5.3/5.3 MB 48.6 MB/s eta 0:00:00
?25hDownloading keras-2.13.1-py3-none-any.whl (1.7 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/1.7 MB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 1.7/1.7 MB 58.5 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.7/1.7 MB 41.7 MB/s eta 0:00:00
?25hDownloading libclang-16.0.6-py2.py3-none-manylinux2010_x86_64.whl (22.9 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/22.9 MB ? eta -:--:--
━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 3.5/22.9 MB 85.0 MB/s eta 0:00:01
━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 6.7/22.9 MB 86.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━ 10.1/22.9 MB 88.9 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━ 13.0/22.9 MB 86.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━ 15.9/22.9 MB 84.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━ 19.3/22.9 MB 83.9 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 22.9/22.9 MB 89.4 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 22.9/22.9 MB 87.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 22.9/22.9 MB 87.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 22.9/22.9 MB 47.9 MB/s eta 0:00:00
?25hDownloading protobuf-4.24.3-cp37-abi3-manylinux2014_x86_64.whl (311 kB)
?25l
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/311.6 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 311.6/311.6 kB 34.8 MB/s eta 0:00:00
?25hDownloading tensorflow_estimator-2.13.0-py2.py3-none-any.whl (440 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/440.8 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 440.8/440.8 kB 54.9 MB/s eta 0:00:00
?25hDownloading tensorflow_io_gcs_filesystem-0.34.0-cp38-cp38-manylinux_2_12_x86_64.manylinux2010_x86_64.whl (2.4 MB)
?25l
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/2.4 MB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 2.4/2.4 MB 61.7 MB/s eta 0:00:00
?25h
Downloading google_auth-2.23.0-py2.py3-none-any.whl (181 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/181.4 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 181.4/181.4 kB 34.4 MB/s eta 0:00:00
?25hDownloading Markdown-3.4.4-py3-none-any.whl (94 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/94.2 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 94.2/94.2 kB 18.0 MB/s eta 0:00:00
?25h
Downloading tensorboard_data_server-0.7.1-py3-none-manylinux2014_x86_64.whl (6.6 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/6.6 MB ? eta -:--:--
━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.9/6.6 MB 44.1 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━ 4.7/6.6 MB 54.6 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╸ 6.6/6.6 MB 61.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 6.6/6.6 MB 49.9 MB/s eta 0:00:00
?25hDownloading werkzeug-2.3.7-py3-none-any.whl (242 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/242.2 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 242.2/242.2 kB 26.7 MB/s eta 0:00:00
?25hUsing cached wheel-0.41.2-py3-none-any.whl (64 kB)
Downloading cachetools-5.3.1-py3-none-any.whl (9.3 kB)
Downloading urllib3-1.26.16-py2.py3-none-any.whl (143 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/143.1 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 143.1/143.1 kB 30.1 MB/s eta 0:00:00
?25h
Installing collected packages: libclang, flatbuffers, wheel, werkzeug, urllib3, typing-extensions, termcolor, tensorflow-io-gcs-filesystem, tensorflow-estimator, tensorboard-data-server, pyasn1, protobuf, oauthlib, numpy, keras, grpcio, google-pasta, gast, cachetools, absl-py, rsa, pyasn1-modules, opt-einsum, markdown, astunparse, requests-oauthlib, google-auth, google-auth-oauthlib, tensorboard, tensorflow
Attempting uninstall: urllib3
Found existing installation: urllib3 2.0.4
Uninstalling urllib3-2.0.4:
Successfully uninstalled urllib3-2.0.4
Attempting uninstall: typing-extensions
Found existing installation: typing_extensions 4.7.1
Uninstalling typing_extensions-4.7.1:
Successfully uninstalled typing_extensions-4.7.1
Attempting uninstall: numpy
Found existing installation: numpy 1.24.4
Uninstalling numpy-1.24.4:
Successfully uninstalled numpy-1.24.4
^C
ERROR: Operation cancelled by user
[notice] A new release of pip is available: 23.0.1 -> 23.2.1
[notice] To update, run: pip install --upgrade pip
Collecting scikit-learn
Obtaining dependency information for scikit-learn from https://files.pythonhosted.org/packages/bf/15/d1b649fc7685d11b806b4546a5438191fb2ad761de70da95ff676189dcec/scikit_learn-1.3.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata
Downloading scikit_learn-1.3.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata (11 kB)
Requirement already satisfied: numpy>=1.17.3 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from scikit-learn) (1.24.3)
Requirement already satisfied: scipy>=1.5.0 in /opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages (from scikit-learn) (1.10.1)
Collecting joblib>=1.1.1 (from scikit-learn)
Obtaining dependency information for joblib>=1.1.1 from https://files.pythonhosted.org/packages/10/40/d551139c85db202f1f384ba8bcf96aca2f329440a844f924c8a0040b6d02/joblib-1.3.2-py3-none-any.whl.metadata
Downloading joblib-1.3.2-py3-none-any.whl.metadata (5.4 kB)
Collecting threadpoolctl>=2.0.0 (from scikit-learn)
Obtaining dependency information for threadpoolctl>=2.0.0 from https://files.pythonhosted.org/packages/81/12/fd4dea011af9d69e1cad05c75f3f7202cdcbeac9b712eea58ca779a72865/threadpoolctl-3.2.0-py3-none-any.whl.metadata
Downloading threadpoolctl-3.2.0-py3-none-any.whl.metadata (10.0 kB)
Downloading scikit_learn-1.3.0-cp38-cp38-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (11.1 MB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/11.1 MB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.1/11.1 MB 3.4 MB/s eta 0:00:04
━━━━━━━╺━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 2.1/11.1 MB 29.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━╸━━━━━━━━━━━━━━━━━━━━━━ 4.9/11.1 MB 46.3 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━━━━━━━━━ 7.8/11.1 MB 56.8 MB/s eta 0:00:01
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╺━━━ 10.0/11.1 MB 56.4 MB/s eta 0:00:01
Also, since the model weights have been stored in chunks, they need to be recombined first:
import importlib
h5tools = importlib.import_module("sf-model-lib.h5tools")
DIR_WEIGHTS = "sf-model-lib/diffusion"
fname_in = [f"{DIR_WEIGHTS}/model_weights_part{j}.h5" for j in [0, 1]]
h5tools.combine(fname_in, fname_out=f"{DIR_WEIGHTS}/model_weights.h5")
Note that to use diffusive_size_factor_AI, Scikit-learn and Tensorflow must be installed. Import necessary packages and the AI model:
import os
import warnings
import h5py
import numpy as np
import openpnm as op
import porespy as ps
import scipy as sp
from matplotlib import pyplot as plt
from sklearn.metrics import r2_score
ps.visualization.set_mpl_style()
warnings.filterwarnings("ignore")
path = "./sf-model-lib/diffusion"
path_train = os.path.join(path, 'g_train_original.hdf5')
path_weights = os.path.join(path, 'model_weights.h5')
g_train = h5py.File(path_train, 'r')['g_train'][()]
model = ps.networks.create_model()
model.load_weights(path_weights)
2023-03-18 21:17:30.719277: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: SSE4.1 SSE4.2
To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags.
[21:17:32] WARNING `lr` is deprecated, please use `learning_rate` instead, or use the legacy optimizer.py:106 optimizer, e.g.,tf.keras.optimizers.legacy.Adam.
Create test image#
We can create a 3D image using PoreSpy’s poly_disperese_spheres generator:
np.random.seed(17)
shape = [120, 120, 120]
dist = sp.stats.norm(loc=7, scale=5)
im = ps.generators.polydisperse_spheres(shape=shape,
porosity=0.7,
dist=dist,
r_min=7)
fig, ax = plt.subplots(1, 1, figsize=[4, 4])
ax.imshow(im[:, :, 20], origin='lower', interpolation='none')
ax.axis(False);
Extract the network#
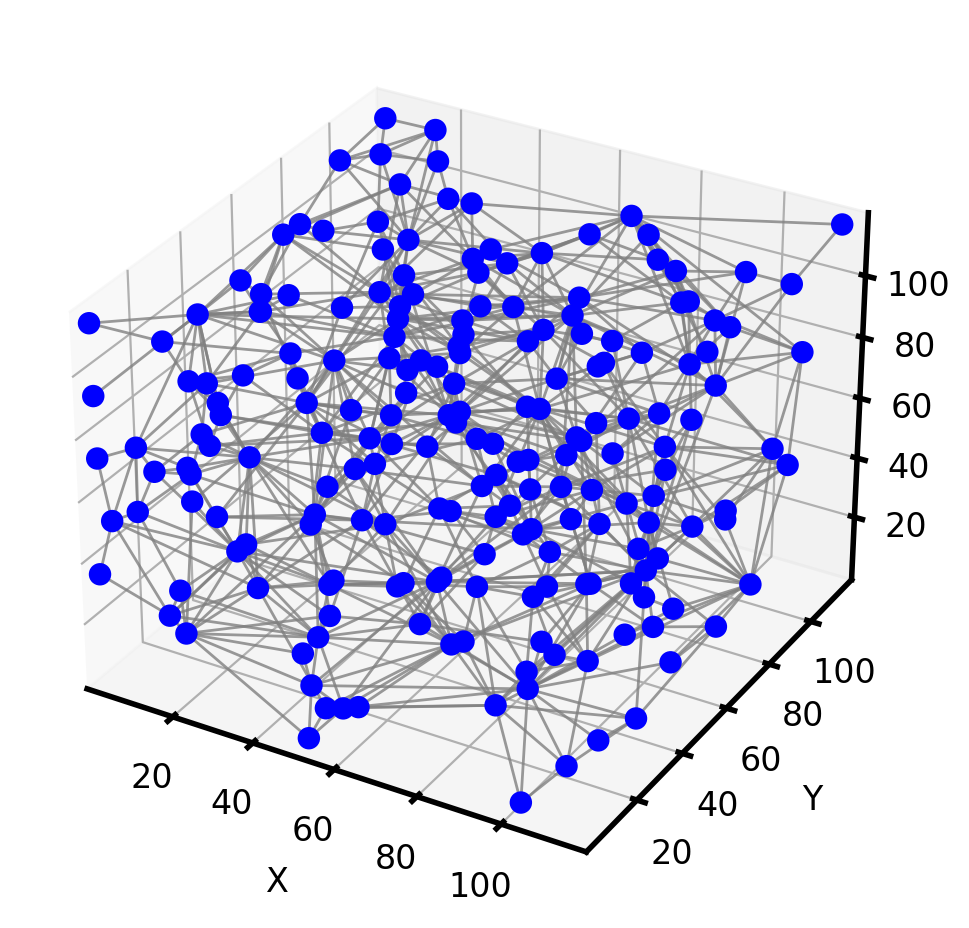
We then extract the pore network of the porous medium image using PoreSpy’s snow2 algorithm. snow2 returns the segmented image of the porous medium as well as extracted network data.
snow = ps.networks.snow2(im, boundary_width=0, parallelization=None)
regions = snow.regions
net = snow.network
Apply diffusive_size_factor_AI#
AI_based diffusive size factors of conduits in the extracted network can then be calculated applying diffusive_size_factor_AI on the segmented regions. We can then define throat.diffusive_size_factor_AI property and assign the predicted size_factor to this property.
conns = net['throat.conns']
size_factors = ps.networks.diffusive_size_factor_AI(regions,
model=model,
g_train=g_train,
throat_conns=conns)
net['throat.diffusive_size_factor_AI'] = size_factors
47/47 [==============================] - 42s 841ms/step
The resulting network can then be imported to OpenPNM for later use such as diffusive mass transport simulations problems. Let’s visualize the network:
pn = op.io.network_from_porespy(net)
fig, ax = plt.subplots(1, 1, figsize=[5, 5])
ax = op.visualization.plot_connections(network=pn, alpha=0.8, color='grey', ax=ax)
ax = op.visualization.plot_coordinates(network=pn, ax=ax, color='b', markersize=50)
Compare with finite difference method#
Now that the extracted network includes AI_based diffusive size factor data, we can use the network to compare the accuracy of diffusive_size_factor_AI, shape factor method,and geometry method (no shape factor) in contrast to finite difference method. Assuming a generic phase with diffusivity of 1, the diffusive conductance of the conduits will be equal to their diffusive size factors. The diffusive conductance of the conduits can be calculated using OpenPNM’s generic_diffusive method. The diffusive conductance of the conduits using shape factor based method assuming cones and cylinders shapes for pores and throats can be calculated as follows:
print(pn)
══════════════════════════════════════════════════════════════════════════════
net : <openpnm.network.Network at 0x7f0256f989a0>
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
# Properties Valid Values
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
2 throat.conns 744 / 744
3 pore.coords 199 / 199
4 pore.region_label 199 / 199
5 pore.phase 199 / 199
6 throat.phases 744 / 744
7 pore.region_volume 199 / 199
8 pore.equivalent_diameter 199 / 199
9 pore.local_peak 199 / 199
10 pore.global_peak 199 / 199
11 pore.geometric_centroid 199 / 199
12 throat.global_peak 744 / 744
13 pore.inscribed_diameter 199 / 199
14 pore.extended_diameter 199 / 199
15 throat.inscribed_diameter 744 / 744
16 throat.total_length 744 / 744
17 throat.direct_length 744 / 744
18 throat.perimeter 744 / 744
19 pore.volume 199 / 199
20 pore.surface_area 199 / 199
21 throat.cross_sectional_area 744 / 744
22 throat.equivalent_diameter 744 / 744
23 throat.diffusive_size_factor_AI 744 / 744
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
# Labels Assigned Locations
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
2 pore.all 199
3 throat.all 744
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
pn['pore.diameter'] = pn['pore.inscribed_diameter']
pn['throat.diameter'] = pn['throat.inscribed_diameter']
pn['throat.coords'] = pn['throat.global_peak']
pn.add_model(propname='throat.length',
model=op.models.geometry.throat_length.hybrid_cones_and_cylinders)
pn.add_model(propname='throat.diffusive_size_factors',
model=op.models.geometry.diffusive_size_factors.cones_and_cylinders,)
phase = op.phase.Phase(network=pn)
phase['pore.diffusivity'] = 1
phase['throat.diffusivity'] = 1
phase.add_model(propname='throat.diffusive_conductance',
model=op.models.physics.diffusive_conductance.generic_diffusive)
g_SF = np.copy(phase['throat.diffusive_conductance'])
To find the diffusive conductance of the conduit using geometry method (no shape factor) we assume cylindrical pores and throats:
cn = pn.conns
L1, Lt, L2 = pn['pore.diameter'][
cn[:, 0]] / 2, pn['throat.length'], pn['pore.diameter'][cn[:, 1]] / 2
D1, Dt, D2 = pn['pore.diameter'][
cn[:, 0]], pn['throat.diameter'], pn['pore.diameter'][cn[:, 1]]
A1, At, A2 = np.pi * D1**2 / 4, np.pi * Dt**2 / 4, np.pi * D2**2 / 4
g_Geo = 1 / (L1 / A1 + L2 / A2 + Lt / At)
The diffusive conductance of the conduit using AI-based method:
phase.add_model(propname='throat.diffusive_conductance',
model=op.models.physics.diffusive_conductance.generic_diffusive,
size_factors='throat.diffusive_size_factor_AI')
g_AI = np.copy(phase['throat.diffusive_conductance'])
The finite difference-based diffusive size factors were calculated using PoreSpy’s size factor method diffusive_size_factor_DNS. However, due to the long runtime of the DNS function the results were saved in the example data folder and used in this example. The Following code was used to estimate the finite difference-based values using PoreSpy:
g_FD = ps.networks.diffusive_size_factor_DNS(regions, conns)
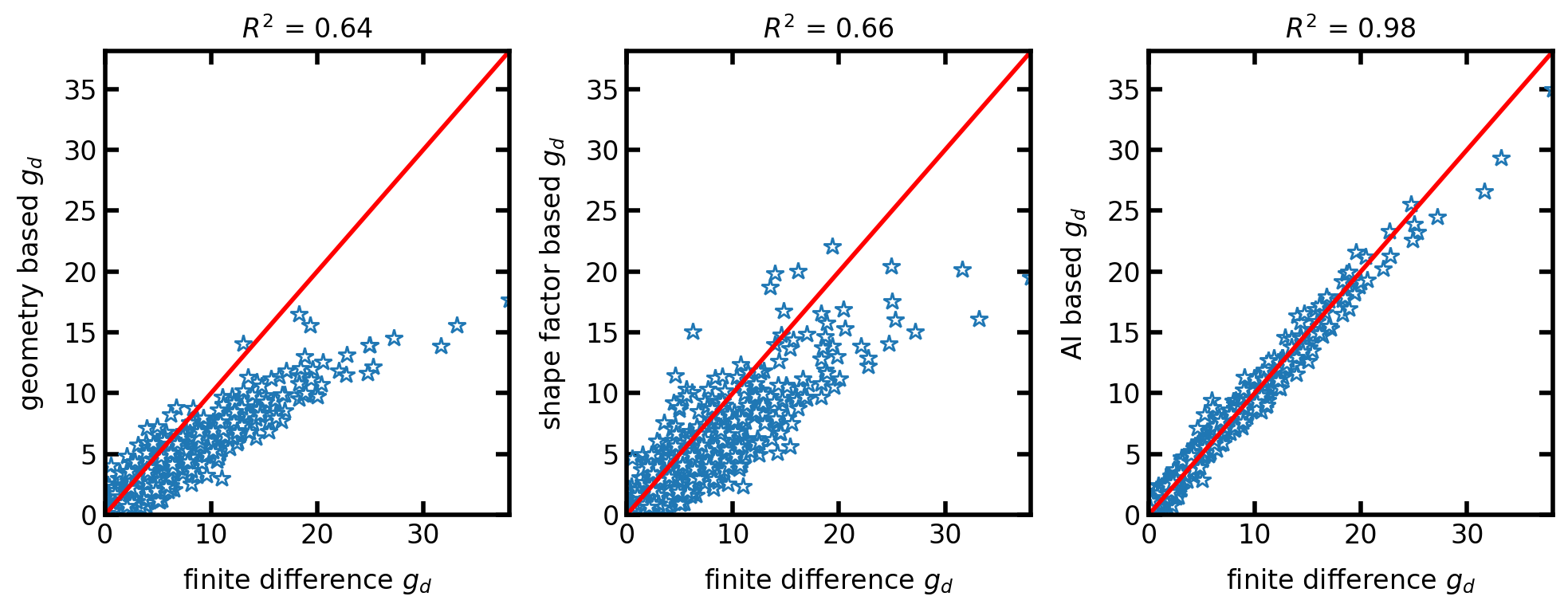
Now let’s compare the diffusive conductance calculated from geometry-based method, shape factor based-method, and AI-based method with reference finite difference method:
fname = os.path.join(path, 'g_finite_difference120-phi7.hdf5')
g_FD = h5py.File(fname, 'r')['g_finite_difference'][()]
max_val = np.max([g_FD, g_AI, g_Geo, g_SF])
fig, ax = plt.subplots(1, 3, figsize=[10, 4])
ax[0].plot(g_FD, g_Geo, '*', [0, max_val], [0, max_val], 'r')
ax[0].set_xlim([0, max_val])
ax[0].set_ylim([0, max_val])
ax[0].set_xlabel('finite difference $g_d$')
ax[0].set_ylabel('geometry based $g_d$')
ax[0].set_title('$R^2$ = ' + str(np.round(r2_score(g_FD, g_Geo), 2)))
ax[1].plot(g_FD, g_SF, '*', [0, max_val], [0, max_val], 'r')
ax[1].set_xlim([0, max_val])
ax[1].set_ylim([0, max_val])
ax[1].set_xlabel('finite difference $g_d$')
ax[1].set_ylabel('shape factor based $g_d$')
ax[1].set_title('$R^2$ = ' + str(np.round(r2_score(g_FD, g_SF), 2)))
ax[2].plot(g_FD, g_AI, '*', [0, max_val], [0, max_val], 'r')
ax[2].set_xlim([0, max_val])
ax[2].set_ylim([0, max_val])
ax[2].set_xlabel('finite difference $g_d$')
ax[2].set_ylabel('AI based $g_d$')
ax[2].set_title(r'$R^2$ = ' + str(np.round(r2_score(g_FD, g_AI), 2)));
As shown in the scatter plots, the AI-based diffusive conductance method predicts the conductance values with a higher accuracy than geometry-based and shape factor-based methods. A comprehensive comparison between these methods for a large dataset can be found here.