snow2#
The SNOW algorithm uses a standard marker-based watershed segementation function to identify pores. The key to the SNOW algorithm is in how the markers are identified. Finding peaks in the distance transform which truly correspond to pore centers requires several careful steps. Each of these steps can be done manually, but the snow2 function was created to combine them all in a single function for ease of use.
In addition to the original SNOW algorithm, snow2 also incorporates a few new developements such as multiphase extractions and parallelized processing. The new snow2 function also handles boundaries better, and returns a different set of geometrical properties. For instance it no longer returns ‘pore.diameter’, which was an opinionated choice that was not appropriate for every case. Instead it returns several different diameters, like ‘pore.equivalent_diameter’ and ‘pore.inscribed_diameter’, and the user must decide which of these they wish to declare as the offical ‘pore.diameter’.
The snow2 function has quite a few arguments, which will be explored and explained in this example.
import matplotlib.pyplot as plt
import numpy as np
import openpnm as op
import scipy.ndimage as spim
from edt import edt
import porespy as ps
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 3
1 import matplotlib.pyplot as plt
2 import numpy as np
----> 3 import openpnm as op
4 import scipy.ndimage as spim
5 from edt import edt
ModuleNotFoundError: No module named 'openpnm'
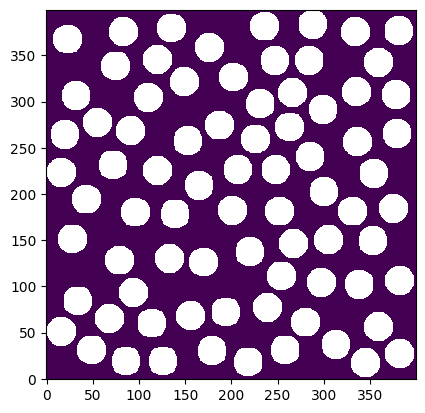
im = ~ps.generators.random_spheres([400, 400], r=15, clearance=5)
ps.imshow(im);
phases#
One of the main features of snow2 is the ability to extract networks from multiple phases simultaneously, and have them be interconnected. This is quite useful for modeling electrochemial devices for instance, since transport occurs in the solid and void phases simultaneously, and the processes are coupled. For a powerful example, see Khan et al. where the transient discharage of a Li-ion battery was modelled using PNMs. Li-ion batteries contain 3 distinct phases: liquid electrolyte, solid active material, and carbonaceous binder.
Note that snow2 does not need to operate on mulitphase phases, only that it can if needed. It accomplishes this flexibility by ignoring all 0’s in the input images, and treating all voxels with values of 1, 2, 3, etc. as distinct phases. Therefore supplying an image of 0’s and 1’s will result in a standard single phase extraction, while supplying an image of 1’s and 2’s will create a dual phase network.
A few additional notes:
It should also be mentioned that the image can contain 0’s as well as values (ie. 1, 2, 3), so can have multiple phases and have some regions ignored
The voxels values do not have be integers or sequential. Each unique numerical value in the image is treated as phase.
Let’s explore this:
im.min()
False
net1 = ps.networks.snow2(phases=im, boundary_width=0)
net2 = ps.networks.snow2(phases=im.astype(int) + 1, boundary_width=0)
The “object” returned by the snow2 function is a dataclass-like object, meaning it has data attached to it as attributes. These attributes are the segmented image called regions, the OpenPNM compatible network called network, and a copy of the input image called phases which will be padded to be the same size as regions if any boundaries were added.
fig, ax = plt.subplots(1, 2, figsize=[12, 6])
ax[0].imshow(net1.regions, origin='lower', interpolation='none')
ax[1].imshow(net2.regions, origin='lower', interpolation='none');
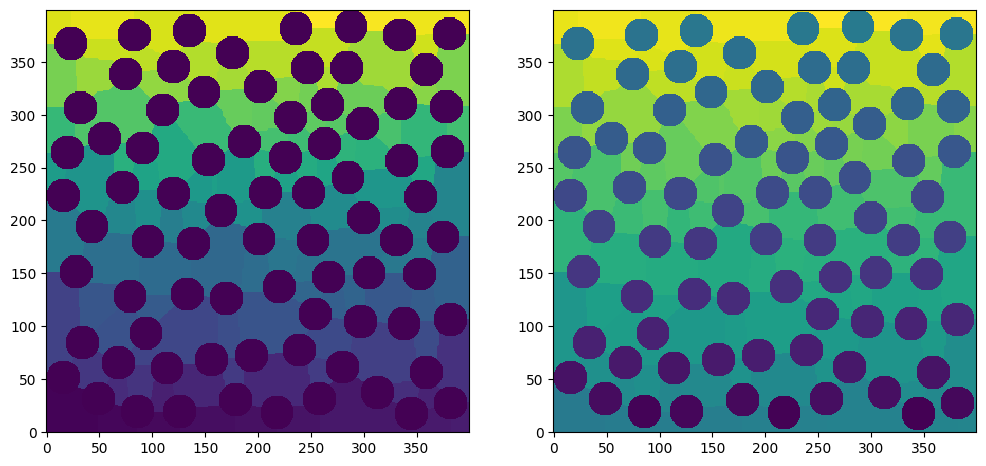
On the left we can see that the spherical particles are all purple, which indicates 0, because they have not been labelled by the function. On the right the particles each have a unique greyscale value because they have been labelled as distinct regions.
The returned objects (net1 and net2) also contain the pore networks, in OpenPNM format. We can overlay these networks with the above images. Let’s start with the single phase network:
pn1 = op.io.network_from_porespy(net1.network)
ax = op.visualization.plot_connections(pn1, c='k')
ax = op.visualization.plot_coordinates(pn1, markersize=50, ax=ax)
fig, ax = plt.gcf(), plt.gca()
ax.imshow(net1.regions.T)
ax.axis(False);
The image needed to be rotated so that the x and y directions lined up with the OpenPNM network. The agreement between the image and network is pretty good. Clearly the the red pore centers lie within each labelled regions and the black throat connections follow the topology quite well.
Now let’s do the same for the multiphase network:
pn2 = op.io.network_from_porespy(net2.network)
ax = op.visualization.plot_connections(pn2, c='k')
ax = op.visualization.plot_coordinates(pn2, markersize=50, ax=ax)
fig, ax = plt.gcf(), plt.gca()
ax.imshow(net2.regions.T)
ax.axis(False);
The above shows the additional network comprised of the solids (although they don’t actually connect in this 2D example) as well as the void-solid connections. We can improve this plot by coloring the different types of pores and throats differently. If we print pn2 we can see that snow2 has created some labels for us, by assuming phase names of “phase1” and “phase2”.
print(pn2)
throat.conns
[[ 0 82]
[ 0 83]
[ 0 90]
...
[183 187]
[184 188]
[186 188]]
<class 'numpy.ndarray'>
int32
pore.coords
[[ 16. 80. 0. ]
[ 16. 251. 0. ]
[ 25. 144. 0. ]
[ 25. 181. 0. ]
[ 33. 379. 0. ]
[ 34. 320. 0. ]
[ 37. 19. 0. ]
[ 40. 109. 0. ]
[ 49. 58. 0. ]
[ 53. 234. 0. ]
[ 59. 197. 0. ]
[ 61. 272. 0. ]
[ 64. 139. 0. ]
[ 71. 316. 0. ]
[ 72. 87. 0. ]
[ 74. 24. 0. ]
[ 74. 367. 0. ]
[ 89. 225. 0. ]
[ 95. 57. 0. ]
[107. 151. 0. ]
[108. 327. 0. ]
[111. 18. 0. ]
[111. 113. 0. ]
[118. 189. 0. ]
[124. 255. 0. ]
[125. 364. 0. ]
[126. 293. 0. ]
[128. 78. 0. ]
[143. 218. 0. ]
[144. 152. 0. ]
[148. 329. 0. ]
[151. 47. 0. ]
[157. 116. 0. ]
[165. 294. 0. ]
[169. 370. 0. ]
[171. 256. 0. ]
[173. 177. 0. ]
[185. 16. 0. ]
[189. 54. 0. ]
[198. 347. 0. ]
[202. 298. 0. ]
[206. 91. 0. ]
[206. 228. 0. ]
[215. 174. 0. ]
[215. 381. 0. ]
[221. 135. 0. ]
[226. 261. 0. ]
[238. 16. 0. ]
[240. 306. 0. ]
[242. 80. 0. ]
[242. 346. 0. ]
[258. 383. 0. ]
[262. 244. 0. ]
[263. 154. 0. ]
[263. 196. 0. ]
[264. 49. 0. ]
[272. 118. 0. ]
[279. 350. 0. ]
[282. 310. 0. ]
[284. 17. 0. ]
[284. 82. 0. ]
[298. 257. 0. ]
[298. 383. 0. ]
[300. 190. 0. ]
[313. 333. 0. ]
[315. 224. 0. ]
[318. 154. 0. ]
[319. 68. 0. ]
[322. 22. 0. ]
[324. 292. 0. ]
[339. 103. 0. ]
[339. 382. 0. ]
[351. 214. 0. ]
[359. 173. 0. ]
[360. 351. 0. ]
[361. 309. 0. ]
[363. 24. 0. ]
[368. 251. 0. ]
[379. 383. 0. ]
[380. 115. 0. ]
[382. 61. 0. ]
[ 13.6402214 8.38929889 0. ]
[ 16.95243978 45.06670784 0. ]
[ 11.97881356 114.99661017 0. ]
[ 7.94285714 162.5 0. ]
[ 21.47852194 213.90808314 0. ]
[ 26.96234613 289.51737871 0. ]
[ 14.15455665 348.89593596 0. ]
[ 12.02626263 390.41616162 0. ]
[ 47.01476793 165.32067511 0. ]
[ 44.01197605 83.39221557 0. ]
[ 41.99463807 252.90884718 0. ]
[ 42.9488189 131.06692913 0. ]
[ 56.65789474 389.17251462 0. ]
[ 52.03517964 346.89296407 0. ]
[ 57.24271845 6.6092233 0. ]
[ 53.36577181 34.5704698 0. ]
[ 75.50932836 112.99813433 0. ]
[ 67.55102041 217.95510204 0. ]
[ 85.64050633 250.21772152 0. ]
[ 72.25609756 54.96493902 0. ]
[ 83.83201941 171.28562765 0. ]
[ 94.43589744 288.27672956 0. ]
[ 89.02554745 202.08394161 0. ]
[ 83.51102941 338.70220588 0. ]
[ 89.7238806 6.6318408 0. ]
[100.17904903 385.71768202 0. ]
[ 91.40268456 133.92170022 0. ]
[100.8411215 85.18457944 0. ]
[ 94.01831502 33.63003663 0. ]
[100.89081456 353.32582322 0. ]
[116.80811078 222.5776459 0. ]
[121.77202073 47.80103627 0. ]
[130.32232497 130.89035667 0. ]
[147.36301793 15.2436611 0. ]
[123.51973684 165.34210526 0. ]
[126.82727273 340.2 0. ]
[127.93602694 316.003367 0. ]
[133.21162791 102.63023256 0. ]
[146.82551143 272.91576414 0. ]
[145.75247525 386.81287129 0. ]
[145.1476378 184.75885827 0. ]
[146.84773663 243.35185185 0. ]
[147.79049676 354.16414687 0. ]
[145.69387755 305.51360544 0. ]
[167.09887006 81.39500942 0. ]
[186.70990566 137.57985175 0. ]
[174.02823529 217.22176471 0. ]
[179.37522124 320.02743363 0. ]
[171.56455142 346.64770241 0. ]
[174.16455696 38.11075949 0. ]
[193.08434959 274.45934959 0. ]
[188.18994413 389.81564246 0. ]
[199.50105708 250.02536998 0. ]
[193.84693878 367.58843537 0. ]
[211.44580777 6.73619632 0. ]
[198.25240055 196.12482853 0. ]
[221.12957198 47.73307393 0. ]
[218.59006816 325.37877313 0. ]
[219.4 357.54647887 0. ]
[234.84110535 215.86183074 0. ]
[237.01089494 108.41400778 0. ]
[223.16995074 287. 0. ]
[235.30508475 392.88418079 0. ]
[235.20491803 154.69262295 0. ]
[237.8125 369.94270833 0. ]
[244.94165316 174.69854133 0. ]
[262.79564411 277.99258573 0. ]
[249.28730512 134.50556793 0. ]
[261.64082687 6.20155039 0. ]
[260.71827411 326.93527919 0. ]
[261.25428571 26.4 0. ]
[259.54230769 360.39230769 0. ]
[263.35294118 70.85661765 0. ]
[264.55882353 93.45454545 0. ]
[278. 393.32713755 0. ]
[284.98479613 221.96406358 0. ]
[275.91420912 178.3538874 0. ]
[287.68421053 143.06791171 0. ]
[278.40310078 372.10077519 0. ]
[296.35091278 47.40162272 0. ]
[291.95294118 165.0907563 0. ]
[307.04719101 111.03505618 0. ]
[291.01532567 331.02681992 0. ]
[305.61748634 6.22131148 0. ]
[310.40641711 360.84278075 0. ]
[300.36998255 285.69458988 0. ]
[306.24585635 310.7320442 0. ]
[319.15789474 393.06578947 0. ]
[333.37347561 252.06097561 0. ]
[330.06184896 188.7890625 0. ]
[333.86480687 312.37339056 0. ]
[345.93449782 46.92212518 0. ]
[343.50704225 7.79225352 0. ]
[342.4457429 330.89983306 0. ]
[335.88076923 355.18461538 0. ]
[349.14293785 137.18587571 0. ]
[348.64447236 75.91331658 0. ]
[351.80164159 282.27770178 0. ]
[358.29824561 393.44210526 0. ]
[359.07758621 372.67241379 0. ]
[367.0311174 91.54879774 0. ]
[382.17356688 210.19785032 0. ]
[385.22014309 340.11172262 0. ]
[386.34341085 22.78682171 0. ]
[384.42998761 281.366171 0. ]
[385.4726477 149.26185266 0. ]
[394.28873239 393.14788732 0. ]
[391.6601626 89.10243902 0. ]]
<class 'numpy.ndarray'>
float64
pore.region_label
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108
109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126
127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144
145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162
163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180
181 182 183 184 185 186 187 188 189]
<class 'numpy.ndarray'>
int32
pore.phase
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2]
<class 'numpy.ndarray'>
int32
throat.phases
[[1 2]
[1 2]
[1 2]
...
[2 2]
[2 2]
[2 2]]
<class 'numpy.ndarray'>
int32
pore.region_volume
[ 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 542. 1619. 1180.
560. 2165. 2762. 1624. 495. 948. 668. 373. 254. 684. 1336. 412.
298. 1072. 245. 1185. 656. 1649. 2067. 548. 544. 402. 1346. 447.
856. 273. 577. 1011. 965. 757. 1617. 304. 330. 297. 430. 831.
1010. 1016. 486. 463. 294. 2124. 2968. 1700. 1130. 457. 316. 984.
716. 473. 294. 489. 729. 2570. 1027. 355. 2316. 1285. 406. 354.
488. 384. 617. 2158. 449. 387. 788. 350. 260. 272. 374. 269.
1447. 373. 589. 258. 1479. 595. 2225. 261. 366. 935. 573. 362.
304. 1968. 1536. 466. 1374. 568. 599. 520. 1770. 796. 731. 285.
232. 707. 2512. 1817. 1290. 1614. 1371. 142. 615.]
<class 'numpy.ndarray'>
float64
pore.equivalent_diameter
[31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 26.26967516 45.40236583 38.76109729
26.70232471 52.50298672 59.30166627 45.47242044 25.10485162 34.74235295
29.16374489 21.79262146 17.98340469 29.51094456 41.24376355 22.90359562
19.47884453 36.94472617 17.66192765 38.84313145 28.90060798 45.82108695
51.30093702 26.41467907 26.31809857 22.62393195 41.39783119 23.85661494
33.01352829 18.6438836 27.10459772 35.87819923 35.05247724 31.04581027
45.3743137 19.67396304 20.49802551 19.44613444 23.39856842 32.52786593
35.86045092 35.96680939 24.87557876 24.27982515 19.34767237 52.00346905
61.47336796 46.52426492 37.93099901 24.12199146 20.05850683 35.3958714
30.19336871 24.5406256 19.34767237 24.95223712 30.46623751 57.20337079
36.16098744 21.26029253 54.30306424 40.44889139 22.73621022 21.23032734
24.92671053 22.11162557 28.02835705 52.41804019 23.90992588 22.19783106
31.67511265 21.11004123 18.19456737 18.60970597 21.82181454 18.50679436
42.92292652 21.79262146 27.38499757 18.12445317 43.3949454 27.52412631
53.22553886 18.22952334 21.58716455 34.50331831 27.01048424 21.46887783
19.67396304 50.05732138 44.22325113 24.35835848 41.82620153 26.89237924
27.61648941 25.73100393 47.47245511 31.83549399 30.50800071 19.0492328
17.18695943 30.00300582 56.55420176 48.09860968 40.52750933 45.33220296
41.78051479 13.44618962 27.98289335]
<class 'numpy.ndarray'>
float64
pore.local_peak
[[ 17. 81.]
[ 17. 252.]
[ 26. 145.]
[ 26. 182.]
[ 34. 380.]
[ 35. 321.]
[ 38. 20.]
[ 41. 110.]
[ 50. 59.]
[ 54. 235.]
[ 60. 198.]
[ 62. 273.]
[ 65. 140.]
[ 72. 317.]
[ 73. 88.]
[ 75. 25.]
[ 75. 368.]
[ 90. 226.]
[ 96. 58.]
[108. 152.]
[109. 328.]
[112. 19.]
[112. 114.]
[119. 190.]
[125. 256.]
[126. 365.]
[127. 294.]
[129. 79.]
[144. 219.]
[145. 153.]
[149. 330.]
[152. 48.]
[158. 117.]
[166. 295.]
[170. 371.]
[172. 257.]
[174. 178.]
[186. 17.]
[190. 55.]
[199. 348.]
[203. 299.]
[207. 92.]
[207. 229.]
[216. 175.]
[216. 382.]
[222. 136.]
[227. 262.]
[239. 17.]
[241. 307.]
[243. 81.]
[243. 347.]
[259. 384.]
[263. 245.]
[264. 155.]
[264. 197.]
[265. 50.]
[273. 119.]
[280. 351.]
[283. 311.]
[285. 18.]
[285. 83.]
[299. 258.]
[299. 384.]
[301. 191.]
[314. 334.]
[316. 225.]
[319. 155.]
[320. 69.]
[323. 23.]
[325. 293.]
[340. 104.]
[340. 383.]
[352. 215.]
[360. 174.]
[361. 352.]
[362. 310.]
[364. 25.]
[369. 252.]
[380. 384.]
[381. 116.]
[383. 62.]
[ 10. 10.]
[ 18. 48.]
[ 13. 109.]
[ 9. 163.]
[ 20. 217.]
[ 21. 288.]
[ 18. 350.]
[ 10. 390.]
[ 49. 164.]
[ 43. 84.]
[ 40. 254.]
[ 44. 132.]
[ 59. 390.]
[ 51. 348.]
[ 59. 8.]
[ 55. 36.]
[ 83. 115.]
[ 69. 218.]
[ 82. 253.]
[ 73. 49.]
[ 80. 171.]
[ 93. 289.]
[ 94. 202.]
[ 84. 341.]
[ 91. 8.]
[102. 385.]
[ 89. 136.]
[101. 86.]
[ 96. 35.]
[101. 355.]
[118. 229.]
[123. 46.]
[134. 129.]
[144. 17.]
[125. 167.]
[128. 342.]
[129. 317.]
[135. 104.]
[147. 274.]
[145. 387.]
[147. 188.]
[149. 245.]
[150. 355.]
[146. 307.]
[166. 82.]
[185. 142.]
[176. 219.]
[180. 323.]
[168. 346.]
[174. 38.]
[196. 272.]
[190. 389.]
[196. 251.]
[192. 370.]
[210. 9.]
[200. 197.]
[225. 50.]
[217. 325.]
[221. 358.]
[231. 205.]
[242. 112.]
[225. 287.]
[237. 393.]
[239. 155.]
[238. 371.]
[244. 176.]
[265. 280.]
[248. 136.]
[262. 9.]
[260. 326.]
[262. 26.]
[260. 362.]
[264. 72.]
[264. 94.]
[279. 394.]
[285. 221.]
[274. 176.]
[288. 145.]
[279. 373.]
[296. 48.]
[291. 166.]
[308. 119.]
[292. 332.]
[306. 8.]
[315. 361.]
[300. 289.]
[307. 310.]
[320. 394.]
[334. 256.]
[332. 189.]
[337. 314.]
[345. 50.]
[344. 9.]
[342. 333.]
[336. 353.]
[351. 138.]
[350. 78.]
[352. 284.]
[360. 394.]
[360. 374.]
[370. 91.]
[383. 199.]
[385. 331.]
[389. 12.]
[383. 283.]
[385. 150.]
[396. 396.]
[391. 87.]]
<class 'numpy.ndarray'>
float64
pore.global_peak
[[ 16. 80.]
[ 16. 251.]
[ 25. 144.]
[ 25. 181.]
[ 33. 379.]
[ 34. 320.]
[ 37. 19.]
[ 40. 109.]
[ 49. 58.]
[ 53. 234.]
[ 59. 197.]
[ 61. 272.]
[ 64. 139.]
[ 71. 316.]
[ 72. 87.]
[ 74. 24.]
[ 74. 367.]
[ 89. 225.]
[ 95. 57.]
[107. 151.]
[108. 327.]
[111. 18.]
[111. 113.]
[118. 189.]
[124. 255.]
[125. 364.]
[126. 293.]
[128. 78.]
[143. 218.]
[144. 152.]
[148. 329.]
[151. 47.]
[157. 116.]
[165. 294.]
[169. 370.]
[171. 256.]
[173. 177.]
[185. 16.]
[189. 54.]
[198. 347.]
[202. 298.]
[206. 91.]
[206. 228.]
[215. 174.]
[215. 381.]
[221. 135.]
[226. 261.]
[238. 16.]
[240. 306.]
[242. 80.]
[242. 346.]
[258. 383.]
[262. 244.]
[263. 154.]
[263. 196.]
[264. 49.]
[272. 118.]
[279. 350.]
[282. 310.]
[284. 17.]
[284. 82.]
[298. 257.]
[298. 383.]
[300. 190.]
[313. 333.]
[315. 224.]
[318. 154.]
[319. 68.]
[322. 22.]
[324. 292.]
[339. 103.]
[339. 382.]
[351. 214.]
[359. 173.]
[360. 351.]
[361. 309.]
[363. 24.]
[368. 251.]
[379. 383.]
[380. 115.]
[382. 61.]
[ 0. 0.]
[ 0. 40.]
[ 0. 115.]
[ 25. 144.]
[ 0. 213.]
[ 0. 292.]
[ 0. 349.]
[ 0. 399.]
[ 25. 144.]
[ 42. 83.]
[ 41. 256.]
[ 31. 143.]
[ 61. 399.]
[ 46. 350.]
[ 37. 19.]
[ 42. 20.]
[ 82. 115.]
[ 55. 230.]
[ 91. 258.]
[ 72. 48.]
[ 79. 170.]
[ 92. 288.]
[ 89. 195.]
[ 84. 341.]
[111. 18.]
[101. 399.]
[ 90. 130.]
[100. 85.]
[104. 20.]
[ 98. 353.]
[117. 228.]
[122. 45.]
[144. 152.]
[147. 0.]
[112. 150.]
[115. 327.]
[116. 325.]
[135. 103.]
[126. 293.]
[143. 399.]
[146. 187.]
[148. 244.]
[149. 354.]
[157. 292.]
[165. 81.]
[184. 141.]
[176. 211.]
[179. 322.]
[171. 343.]
[188. 51.]
[202. 297.]
[186. 399.]
[199. 255.]
[193. 371.]
[185. 16.]
[184. 206.]
[224. 49.]
[240. 306.]
[220. 357.]
[230. 204.]
[241. 111.]
[224. 286.]
[215. 381.]
[237. 157.]
[251. 382.]
[243. 175.]
[264. 279.]
[248. 131.]
[238. 16.]
[242. 346.]
[261. 25.]
[249. 347.]
[251. 78.]
[278. 81.]
[258. 383.]
[262. 244.]
[263. 194.]
[301. 129.]
[290. 381.]
[295. 47.]
[290. 163.]
[307. 119.]
[280. 343.]
[284. 17.]
[298. 383.]
[296. 285.]
[306. 309.]
[298. 383.]
[333. 255.]
[331. 188.]
[335. 317.]
[349. 54.]
[322. 22.]
[341. 329.]
[332. 354.]
[351. 137.]
[351. 72.]
[337. 262.]
[339. 382.]
[348. 380.]
[351. 72.]
[399. 202.]
[399. 331.]
[399. 0.]
[399. 284.]
[399. 155.]
[379. 383.]
[399. 89.]]
<class 'numpy.ndarray'>
float64
pore.geometric_centroid
[[ 16. 80. ]
[ 16. 251. ]
[ 25. 144. ]
[ 25. 181. ]
[ 33. 379. ]
[ 34. 320. ]
[ 37. 19. ]
[ 40. 109. ]
[ 49. 58. ]
[ 53. 234. ]
[ 59. 197. ]
[ 61. 272. ]
[ 64. 139. ]
[ 71. 316. ]
[ 72. 87. ]
[ 74. 24. ]
[ 74. 367. ]
[ 89. 225. ]
[ 95. 57. ]
[107. 151. ]
[108. 327. ]
[111. 18. ]
[111. 113. ]
[118. 189. ]
[124. 255. ]
[125. 364. ]
[126. 293. ]
[128. 78. ]
[143. 218. ]
[144. 152. ]
[148. 329. ]
[151. 47. ]
[157. 116. ]
[165. 294. ]
[169. 370. ]
[171. 256. ]
[173. 177. ]
[185. 16. ]
[189. 54. ]
[198. 347. ]
[202. 298. ]
[206. 91. ]
[206. 228. ]
[215. 174. ]
[215. 381. ]
[221. 135. ]
[226. 261. ]
[238. 16. ]
[240. 306. ]
[242. 80. ]
[242. 346. ]
[258. 383. ]
[262. 244. ]
[263. 154. ]
[263. 196. ]
[264. 49. ]
[272. 118. ]
[279. 350. ]
[282. 310. ]
[284. 17. ]
[284. 82. ]
[298. 257. ]
[298. 383. ]
[300. 190. ]
[313. 333. ]
[315. 224. ]
[318. 154. ]
[319. 68. ]
[322. 22. ]
[324. 292. ]
[339. 103. ]
[339. 382. ]
[351. 214. ]
[359. 173. ]
[360. 351. ]
[361. 309. ]
[363. 24. ]
[368. 251. ]
[379. 383. ]
[380. 115. ]
[382. 61. ]
[ 13.6402214 8.38929889]
[ 16.95243978 45.06670784]
[ 11.97881356 114.99661017]
[ 7.94285714 162.5 ]
[ 21.47852194 213.90808314]
[ 26.96234613 289.51737871]
[ 14.15455665 348.89593596]
[ 12.02626263 390.41616162]
[ 47.01476793 165.32067511]
[ 44.01197605 83.39221557]
[ 41.99463807 252.90884718]
[ 42.9488189 131.06692913]
[ 56.65789474 389.17251462]
[ 52.03517964 346.89296407]
[ 57.24271845 6.6092233 ]
[ 53.36577181 34.5704698 ]
[ 75.50932836 112.99813433]
[ 67.55102041 217.95510204]
[ 85.64050633 250.21772152]
[ 72.25609756 54.96493902]
[ 83.83201941 171.28562765]
[ 94.43589744 288.27672956]
[ 89.02554745 202.08394161]
[ 83.51102941 338.70220588]
[ 89.7238806 6.6318408 ]
[100.17904903 385.71768202]
[ 91.40268456 133.92170022]
[100.8411215 85.18457944]
[ 94.01831502 33.63003663]
[100.89081456 353.32582322]
[116.80811078 222.5776459 ]
[121.77202073 47.80103627]
[130.32232497 130.89035667]
[147.36301793 15.2436611 ]
[123.51973684 165.34210526]
[126.82727273 340.2 ]
[127.93602694 316.003367 ]
[133.21162791 102.63023256]
[146.82551143 272.91576414]
[145.75247525 386.81287129]
[145.1476378 184.75885827]
[146.84773663 243.35185185]
[147.79049676 354.16414687]
[145.69387755 305.51360544]
[167.09887006 81.39500942]
[186.70990566 137.57985175]
[174.02823529 217.22176471]
[179.37522124 320.02743363]
[171.56455142 346.64770241]
[174.16455696 38.11075949]
[193.08434959 274.45934959]
[188.18994413 389.81564246]
[199.50105708 250.02536998]
[193.84693878 367.58843537]
[211.44580777 6.73619632]
[198.25240055 196.12482853]
[221.12957198 47.73307393]
[218.59006816 325.37877313]
[219.4 357.54647887]
[234.84110535 215.86183074]
[237.01089494 108.41400778]
[223.16995074 287. ]
[235.30508475 392.88418079]
[235.20491803 154.69262295]
[237.8125 369.94270833]
[244.94165316 174.69854133]
[262.79564411 277.99258573]
[249.28730512 134.50556793]
[261.64082687 6.20155039]
[260.71827411 326.93527919]
[261.25428571 26.4 ]
[259.54230769 360.39230769]
[263.35294118 70.85661765]
[264.55882353 93.45454545]
[278. 393.32713755]
[284.98479613 221.96406358]
[275.91420912 178.3538874 ]
[287.68421053 143.06791171]
[278.40310078 372.10077519]
[296.35091278 47.40162272]
[291.95294118 165.0907563 ]
[307.04719101 111.03505618]
[291.01532567 331.02681992]
[305.61748634 6.22131148]
[310.40641711 360.84278075]
[300.36998255 285.69458988]
[306.24585635 310.7320442 ]
[319.15789474 393.06578947]
[333.37347561 252.06097561]
[330.06184896 188.7890625 ]
[333.86480687 312.37339056]
[345.93449782 46.92212518]
[343.50704225 7.79225352]
[342.4457429 330.89983306]
[335.88076923 355.18461538]
[349.14293785 137.18587571]
[348.64447236 75.91331658]
[351.80164159 282.27770178]
[358.29824561 393.44210526]
[359.07758621 372.67241379]
[367.0311174 91.54879774]
[382.17356688 210.19785032]
[385.22014309 340.11172262]
[386.34341085 22.78682171]
[384.42998761 281.366171 ]
[385.4726477 149.26185266]
[394.28873239 393.14788732]
[391.6601626 89.10243902]]
<class 'numpy.ndarray'>
float64
throat.global_peak
[[ 0. 75. 0.]
[ 0. 81. 0.]
[ 27. 92. 0.]
...
[399. 383. 0.]
[399. 62. 0.]
[399. 115. 0.]]
<class 'numpy.ndarray'>
float64
pore.inscribed_diameter
[32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 20. 36. 26.
18. 40. 40.2492218 34.05877304 20. 26.07680893
20.39607811 15.62049961 12.80624866 22. 31.1126976 15.62049961
14.42220497 26. 12.64911079 24.73863411 17.88854408 35.6089859
38. 18. 20.88061333 15.62049961 31.1126976 18.
26. 14.14213562 22.36067963 24.16609192 26.83281517 21.54065895
32.55764008 14.14213562 15.62049961 14.42220497 18.86796188 25.45584488
26.90724754 26. 20.39607811 19.79899025 14.42220497 40.44749832
42.42640686 33.10589218 31.24099922 18. 15.62049961 24.33105087
22.36067963 17.88854408 14. 18. 22. 40.
26.90724754 17.08800697 35.77708817 31.1126976 18.86796188 16.
19.79899025 17.88854408 22. 40. 18.11077118 17.08800697
22.62741661 17.08800697 14. 14. 16.12451553 13.41640759
32. 15.2315464 18.97366524 14. 32. 22.09072113
39.39543152 13.41640759 14.14213562 24. 20. 17.88854408
14. 40. 32. 16.4924221 31.24099922 18.
22. 20. 39.84971619 24.08318901 24.16609192 13.41640759
12.64911079 23.32380676 36. 31.1126976 24. 36.
32. 8.48528099 20. ]
<class 'numpy.ndarray'>
float64
pore.extended_diameter
[32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 51.88448715 53.66563034 45.25483322
32. 49.67897034 56.46237564 58. 45.65084839 32.
20.39607811 18.86796188 20. 37.20215225 32.24903107 32.
22. 27.85677719 23.32380676 34.92849731 17.88854408 35.6089859
38. 28.07133675 24.16609192 32. 52.34500885 22.62741661
26. 17.88854408 24.16609192 24.16609192 26.83281517 32.
49.1934967 22. 18. 16. 19.69771576 32.
46.69047165 26. 20.59126091 19.79899025 16. 40.44749832
42.42640686 36.22154236 31.24099922 22.36067963 26. 30.
35.77708817 24.08318901 17.08800697 32. 30.4630928 40.
32. 17.08800697 35.77708817 31.1126976 18.86796188 32.
22. 18. 26. 40. 23.32380676 32.
32. 17.08800697 18. 14. 20. 32.
32. 28. 28.84440994 16. 32. 25.29822159
40. 18. 32. 32. 26. 18.
32. 40. 32. 22.80350876 34.92849731 32.
25.45584488 25.45584488 40.49691391 34. 34. 32.
14. 34. 67.20118713 56.35601044 54.91812134 59.36328888
56.35601044 32. 32.80244064]
<class 'numpy.ndarray'>
float64
throat.inscribed_diameter
[ 2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 44. 8.
2. 7.21110249 8.24621105 20. 5.65685415 5.65685415
20. 6. 2. 6.3245554 8.24621105 6.
38. 17.88854408 6. 14. 36. 28.
10. 8. 28. 7.21110249 5.65685415 8.
7.21110249 10.19803905 34. 20. 6. 18.
10. 21.54065895 14.42220497 6. 8.48528099 32.98484421
14.14213562 5.65685415 7.21110249 28. 12.16552544 8.
6. 6.3245554 8. 14.14213562 19.79899025 6.
6. 20. 40. 8. 7.21110249 7.21110249
10. 8.24621105 5.65685415 10. 17.20465088 5.65685415
6. 16. 6. 14.14213562 2. 12.80624866
10. 8.94427204 10. 15.62049961 16. 8.
8. 14. 28. 5.65685415 18.43908882 14.42220497
14.42220497 6.3245554 23.32380676 8. 8.94427204 12.
14.14213562 8. 12.80624866 27.78488731 20.88061333 6.
18. 5.65685415 8. 24. 11.66190338 16.
6. 6.3245554 5.65685415 22. 2. 24.
6. 10. 5.65685415 14. 8. 10.
11.31370831 21.54065895 8.24621105 18. 20.88061333 16.97056198
14.56021976 12. 2. 19.69771576 13.41640759 8.24621105
12. 12. 6. 22.80350876 6. 16.
4. 6. 10. 5.65685415 7.21110249 12.
6.3245554 6.3245554 10. 2. 6. 4.47213602
4.47213602 19.79899025 24. 25.61249733 6.3245554 5.65685415
8. 16. 8.94427204 22.36067963 8.24621105 5.65685415
5.65685415 14. 10. 23.32380676 14.42220497 11.31370831
10. 4. 6. 28.28427124 8.24621105 12.64911079
10. 21.54065895 8.94427204 10. 32. 10.
18. 17.88854408 12. 4.47213602 10.19803905 29.73213768
28.28427124 28. 10. 2. 5.65685415 24.
32. 50. 46. 10. 4. 8. ]
<class 'numpy.ndarray'>
float64
throat.total_length
[51.16344987 52.07648937 35.34453018 55.37934693 63.01655635 31.68268361
40.95057316 34.53017947 37.70908971 27.6951548 30.30438213 50.29255751
37.048434 42.02786372 28.45258244 40.36504811 40.2118794 43.77578561
45.15068695 36.25135831 26.01758366 41.42260757 36.56195864 26.53695198
33.05521097 35.2504025 28.75624347 42.06131525 34.6644879 32.28830769
28.71778592 35.67637163 38.4121247 27.43693363 27.82992826 44.40441842
47.47360858 39.41195917 27.78114742 40.17455455 35.25038109 45.61421233
26.9812432 44.51766502 45.20029854 39.62029805 22.60405926 41.53485664
43.3615994 32.7806152 52.084621 45.16919715 47.52074199 29.35125565
28.8316495 37.85388258 36.91494164 38.31200851 29.17695096 29.52200712
37.38200174 31.78329119 25.60334376 32.496721 33.00502544 32.20890416
42.31973412 31.40785162 22.58310498 40.60710342 31.79407204 34.26415839
24.12994565 38.34461444 28.97577777 35.5007564 43.04504296 26.64893031
37.01251444 26.69578326 48.30869584 35.49875057 31.12360584 26.98130299
27.98425603 25.03293294 28.94695111 39.68118341 54.69965934 36.88437733
28.66875876 32.11659231 36.44127443 30.34461985 38.93805818 32.33080671
39.9810112 29.77490364 39.18124167 39.12360827 45.48080797 37.05318593
37.03795803 29.31988193 37.72535252 26.66028507 30.00310654 36.92560859
28.26628678 32.32961711 29.53291766 37.22222677 24.98785599 33.28529858
36.32667414 32.10496244 48.31868348 30.74897277 40.00776353 32.53284886
37.87877921 33.03922743 30.07425063 40.33074984 52.26755848 29.28252542
25.73311684 33.3002654 29.40738041 40.03426365 30.05432403 31.20713498
37.3626286 50.14877414 27.64115477 35.17583182 28.19597843 47.20046216
51.91859894 32.99361356 27.97887958 41.52746188 40.83563718 36.28513903
28.78614228 31.51625616 35.56560971 29.33439894 33.92350312 27.94131782
46.50902521 40.33410648 33.52814604 34.17761617 54.60249573 46.95693083
31.82356115 38.81226441 26.39091912 43.29023799 52.95440042 47.24137753
27.71439023 50.56093527 34.28154791 28.18670222 28.6688384 35.54586524
29.51525577 39.99265508 36.6110703 36.98084903 25.44877134 40.12258567
51.83851423 52.45192954 39.38729124 33.74790878 27.26824997 36.41834766
40.9149084 50.50134347 36.2632252 51.66673975 33.7987506 35.72831819
34.30526897 25.43935765 30.74526791 35.77017252 27.09147238 36.56158243
41.02947102 32.74482935 32.26330844 38.28457927 28.84295554 52.53051003
32.48832691 46.4151423 28.14598022 46.77661722 40.44070217 27.54908887
39.30221846 30.78763952 47.75267699 36.35773706 44.46154422 40.70352413
28.39133094 27.11918718 34.05264162 28.47261081 30.02794561 35.98624015
25.67488415 27.93812884 25.84353397 27.99182655 36.78897228 25.74613332
42.45149182 46.03313629 38.82954819 29.85999757 28.23530833 25.92236301
30.58236429 37.0891923 33.2320047 44.43884452 28.22970413 40.13739472
28.05860768 43.89155886 29.71359758 28.11057764 41.49225975 36.2980856
28.30054678 29.31928281 38.1648743 46.29353406 34.97130579 27.93669352
28.31527745 26.57183803 37.91605826 43.95989859 34.72803392 27.23727446
30.74429716 30.97394364 25.36893056 27.56998968 43.56681423 37.29957247
24.46606068 28.9524191 46.31071698 48.41571928 49.08056995 44.65905051
33.14626826 44.95866965 27.07473566 23.67236264 38.10091387 37.04444335
45.25962118 27.22970771 29.52149534 42.92186236 23.469616 38.66959078
28.70805375 33.28871986 35.86353336 31.8828829 31.0882636 46.01215928
45.34596335 32.25923155 30.2708387 47.24380038 45.0150486 37.88543147
33.71946151 52.71661009 41.57081177 36.69357376 45.17539865 27.54852832
42.51392143 36.61643158 24.50393712 27.0743418 50.85724729 32.2578611
32.13203474 37.36414207 45.63440737 39.42220265 32.31628637 37.24851443
27.71381533 33.05982608 35.82918778 27.12709318 49.86401668 37.56851857
46.2781622 41.24939513 43.77560762 49.95974192 36.06478808 28.29863549
29.02189094 27.78393331 40.78490694 30.69525457 28.73167147 35.0045701
44.54784566 39.13906454 38.94687599 28.50248965 42.82446691 36.35087829
36.24511009 50.90989023 40.443077 27.45181456 23.37883157 49.29581039
31.47191565 47.74376044 33.1290575 42.69702152 30.57772359 38.78650096
37.32974579 35.24747702 43.30240715 32.15908664 48.173627 46.11490109
75.77670197 46.9371852 37.90751594 51.51278023 45.61789792 35.0234697
59.51927028 39.33957467 89.87839487 56.47746609 44.40401066 46.30011284
72.87241622 39.58148304 66.57255541 68.30031538 49.8476002 38.17698816
48.28017588 34.49822249 37.30074801 43.50517856 40.87218884 43.78580622
37.43956576 42.70588395 49.28888311 32.55449392 28.2330024 35.07877927
28.09164828 26.65114724 38.25035719 37.4909524 27.22400938 39.94328414
43.67105782 42.07911371 30.69707691 31.24234254 38.70037217 40.70111835
51.70536503 43.6582874 55.49642974 35.92784065 23.17229422 27.33966858
61.71464966 32.56734459 52.24651695 39.04893539 42.8782133 36.78280249
31.16497168 29.09484118 47.3179675 36.7724061 41.58822038 56.55871733
35.22033335 28.68317273 56.79360078 35.26311872 67.8970308 29.11381245
24.24881097 25.21476499 20.68876479 40.00223479 29.56575712 32.69985647
46.3626416 32.71227935 47.52285265 63.43187805 43.48053753 38.29176275
25.12470472 36.89260742 60.98306175 44.12628991 65.82180453 59.67485934
59.96020785 53.02011347 42.16681978 32.31091607 27.884307 48.17114281
39.57953312 30.59379948 49.67309163 25.29238421 33.17345728 22.93592976
49.53806482 51.42834925 27.47667578 42.63287002 51.83598398 41.74201585
64.29105027 45.4442762 48.14203525 32.23068171 38.65879878 42.1589835
22.22385827 43.03294579 69.35705425 50.53369246 28.8395517 31.46982728
40.82620585 23.10933924 44.29349148 22.35770791 24.71567401 23.76068779
31.438006 48.99685548 61.2045399 38.36728536 39.68694651 20.22088642
45.70405057 33.47772019 30.57979549 41.00209765 22.23479708 22.70123917
40.5991404 46.02287592 21.23456617 42.76595624 44.74088302 57.87875277
55.99092911 20.91427423 22.43606608 37.71353995 34.24647274 64.55740112
42.21355492 49.77428244 45.32864348 50.27227157 55.69934166 35.90206993
25.49431147 40.39989259 33.55448403 26.10625393 25.78878967 47.13899442
27.84812126 40.79312154 63.42135415 35.40284322 64.36217696 55.09958048
57.11175685 20.55803024 35.16785565 39.51823699 29.52655691 50.90158299
53.83786147 26.02109262 44.8222498 29.21986675 49.01900999 38.28632918
25.06738532 32.8714111 20.79151355 37.84284639 42.83116468 25.12963739
77.84357408 68.14852029 65.30211054 56.23582092 69.28386431 63.75322651]
<class 'numpy.ndarray'>
float64
throat.direct_length
[34.92849839 35.21363372 28.19574436 37.48332963 40.03748244 26.03843313
31.78049716 25.13961018 30.62678566 22.11334439 25.13961018 33.07567082
27. 35.51056181 23.85372088 25.72936066 37.30951621 31.27299154
35.02855978 32.37282811 25.63201124 32.86335345 23.70653918 22.56102835
28.63564213 25.90366769 22.22611077 35.70714214 34.55430509 25.84569597
23.8117618 23.43074903 37.36308338 21.86321111 21.63330765 36.44173432
41.1339276 33.85262176 22.627417 35.73513677 30.43024811 38.26225294
26.92582404 32.87856445 37.16180835 31.30495168 22.47220505 28.42534081
37.88139385 27.83882181 51.38093031 36.23534186 36.29049462 25.90366769
28.21347196 26.21068484 32.03123476 28.87905816 24.12467616 23.15167381
31. 23.40939982 22.18107301 28.12472222 29.76575213 29.83286778
32.17141588 30.14962686 22.56102835 25.41653005 22.91287847 27.89265136
22.82542442 28.77498914 23.36664289 28.28427125 30.77336511 23.10844002
30.77336511 21.84032967 41.01219331 27.11088342 27.25802634 22.97825059
22.737634 24.10394159 23.06512519 31.68595904 36.45545227 35.48239
28.65309756 29.59729717 26.32489316 24.49489743 38.47076812 31.78049716
33.58571125 24.2693222 27.44084547 38.63935817 44.50842617 33.19638535
29. 25.63201124 32.96968304 26.34387974 23.85372088 30.82207001
24.79919354 31.90611227 23.06512519 28.91366459 23.3023604 28.0713377
30.8058436 25.15949125 39.23009049 26.57066051 33.28663395 25.61249695
31.01612484 25.13961018 24.43358345 32.77193922 45.06661736 23.93741841
23.87467277 25.15949125 23.57965225 32.61901286 29.42787794 29.22327839
31.95309062 37.97367509 24.79919354 30.52867504 27.25802634 36.02776707
36.70149861 27.82085549 22.44994432 29.71531592 34.19064199 28.67054237
26.43860813 23.47338919 27.5680975 24.93992783 29.49576241 27.23967694
38.88444419 28.75760769 29.10326442 28.89636655 41.71330723 40.22437072
31.65438358 37.62977544 24.59674775 28. 48.07286137 35.05709629
21.72556098 32.72613634 32.75667871 26.41968963 20.97617696 29.83286778
23.83275058 31.55946768 25.15949125 32. 23.85372088 40.06245125
50.40833264 45.82575695 35.55277767 33.73425559 22.95648057 32.80243893
31.27299154 46.10856753 27.73084925 46.31414471 27.92848009 29.93325909
28.19574436 25.01999201 23.85372088 23.51595203 25.33771892 34.36568055
31.01612484 24.24871131 28.28427125 35.55277767 28.67054237 45.98912915
26.15339366 40.5092582 28.10693865 35.91656999 25.57342371 25.45584412
28.86173938 25.37715508 36.0970913 29.44486373 38.41874542 28.82707061
23.19482701 26.2488095 31.19294792 25.35744467 24.2899156 26.70205985
22.6715681 24.73863375 24.0208243 22.64950331 22.49444376 23.10844002
39.08964057 33.98529094 31.82766093 27.78488798 27.45906044 23.83275058
27.54995463 26.98147513 31. 34.43835072 27.91057147 34.0147027
21.84032967 42.87190222 22.737634 21.84032967 32.37282811 36.26292873
28.05352028 25.63201124 29.54657341 35.7211422 29.41088234 22.04540769
22.09072203 22.42766149 33.21144381 37.30951621 27.16615541 22.86919325
30.4466747 24.22808288 24.79919354 24.59674775 32.80243893 24.14539294
23.4520788 22.53885534 36.72873534 37.06750599 40.9756025 37.36308338
28.77498914 35.70714214 22.49444376 22.4053565 25.35744467 23.40939982
35.29872519 26.73948391 26.15339366 30.06659276 22.04540769 27.94637722
23.23790008 29.3257566 29.51270913 31.85906464 30.06659276 33.52610923
38.27531842 32.21800739 28.3019434 44.31703961 36.81032464 35.36947837
30.59411708 44.65422712 34.19064199 30.65941943 36.08323711 22.71563338
34.53983208 25.74878638 24.43358345 25.78759392 41.01219331 22.627417
29.42787794 32.92415527 35.63705936 28.74021573 30.2654919 35.55277767
22.69361144 26.98147513 22.4053565 22.13594362 41.92851059 32.75667871
31.38470965 32.95451411 37.13488926 43.8178046 35.53871129 26.68332813
24.45403852 21.65640783 27.45906044 27.33130074 28.68797658 28.24889378
39.40812099 36.20773398 28.56571371 25.3179778 23.34523506 34.62657939
35.21363372 43.17406629 34.51086785 23.17326045 22.4053565 43.32435804
18.30300522 38. 26.77685568 34.66987165 28.37252192 38.70400496
36.52396474 34.0147027 38.44476557 29.69848481 36.81032464 43.63484846
70.09992867 46.9041576 37.88139385 47.66550115 44.98888752 34.88552709
53.15072906 39.1535439 75.80237463 54.88169094 44.05678154 46.23851209
60.73713856 39.56008089 62.6019169 67.47592163 41.55718951 37.92097045
44.63182721 34.4818793 37.28270376 43.22036557 40.06245125 43.71498599
37.22902094 42.52058325 43.64630569 32.51153641 28.21347196 32.48076354
27.76688675 26.2488095 37.60319135 36.97296309 26.68332813 39.05124838
41.64132563 41.59326869 30.46309242 31.20897307 38.11823711 40.1248053
51.58488151 43.47413024 54.5802162 34.49637662 22.69361144 27.31300057
58.27520914 32.38826948 45.57411546 39.0256326 42.83689998 36.7559519
31.144823 29.05167809 47.2546294 36.51027253 41.38840417 56.4092191
35.09985755 28.39013913 56.77147171 35.21363372 64.63745044 29.05167809
24.20743687 25.15949125 20.61552813 39.97499218 29.563491 32.60368077
46.27094121 32.69556545 42.53234064 62.86493458 43.43961326 37.68288736
24.91987159 36.66060556 59.49789912 43.84062043 63.65532185 59.66573556
58.13776741 51.41011574 41.52107898 32.10918872 27.73084925 47.57099957
39.56008089 30.56141358 47.92702787 25.25866188 32.58834147 22.93468988
47.20169488 49.1426495 27.4226184 42.10700654 50.18964037 41.55718951
62.72160712 45.43126677 48.12483766 32.15587038 38.62641583 42.14261501
22.18107301 42.3792402 68.12488532 50.5074252 28.80972058 31.32091953
40.63249931 23.06512519 42.68489194 22.22611077 24.59674775 23.72762104
31.17691454 48.97958759 60.25777958 38.34057903 39.33192088 20.174241
43.96589587 33.46640106 30.5450487 40.8900966 22.18107301 22.60530911
40.47221269 45.97825573 21.21320344 41.14608122 44.53088816 56.97367813
55.95533933 20.78460969 22.42766149 37.41657387 33.91164992 64.52131431
42.19004622 49.57822102 44.86646855 49.54795657 54.4334456 35.55277767
25.33771892 37.90778284 33.37663854 26.07680962 25.69046516 47.11687596
27.64054992 39.12799509 63.34824386 35.38361203 64.28841264 55.00909016
56.32938842 20.39607805 35.0142828 39.19183588 29.10326442 47.05316142
45.36518489 25.13961018 43.73785546 29.03446228 49. 38.26225294
24.12467616 32.61901286 20.76053949 35.98610843 41.74925149 24.71841419
71.19691005 61.01639124 58.74521257 53.79591063 66.52067348 60.47313453]
<class 'numpy.ndarray'>
float64
throat.perimeter
[36. 33. 23. 37. 37. 18. 29. 24. 24. 15. 24. 38. 30. 23. 23. 29. 17. 44.
24. 24. 23. 28. 25. 16. 28. 23. 18. 23. 28. 23. 17. 24. 33. 20. 16. 23.
28. 18. 14. 17. 15. 38. 9. 19. 26. 18. 15. 22. 20. 17. 19. 22. 33. 18.
24. 24. 19. 25. 20. 14. 22. 21. 15. 17. 27. 13. 24. 11. 16. 30. 23. 23.
26. 24. 17. 25. 34. 20. 20. 18. 26. 17. 19. 15. 15. 25. 13. 19. 35. 23.
10. 20. 23. 16. 21. 8. 22. 17. 24. 20. 16. 21. 21. 14. 22. 16. 19. 19.
16. 37. 19. 23. 13. 26. 23. 19. 24. 27. 22. 20. 23. 29. 12. 24. 27. 13.
11. 22. 18. 23. 5. 24. 23. 30. 15. 19. 10. 23. 40. 26. 15. 30. 21. 25.
11. 23. 18. 15. 20. 12. 23. 23. 14. 22. 34. 23. 13. 34. 14. 24. 20. 35.
18. 39. 15. 20. 21. 21. 15. 23. 33. 20. 16. 27. 19. 25. 21. 23. 21. 16.
32. 27. 17. 17. 11. 20. 29. 10. 19. 22. 12. 37. 21. 17. 17. 13. 12. 24.
18. 25. 23. 34. 24. 11. 27. 13. 32. 20. 38. 29. 14. 11. 22. 11. 19. 26.
14. 23. 15. 18. 24. 12. 31. 33. 28. 19. 14. 18. 11. 18. 12. 33. 13. 26.
20. 25. 21. 19. 27. 19. 11. 17. 16. 29. 23. 15. 19. 14. 21. 29. 23. 14.
7. 19. 23. 14. 30. 25. 12. 18. 26. 36. 22. 24. 19. 27. 24. 14. 31. 23.
28. 14. 20. 30. 19. 26. 17. 7. 20. 3. 31. 37. 24. 12. 14. 21. 22. 23.
31. 26. 18. 17. 24. 21. 24. 23. 20. 9. 23. 21. 19. 26. 28. 21. 17. 11.
23. 21. 23. 14. 26. 31. 35. 28. 24. 26. 14. 15. 22. 18. 37. 20. 11. 18.
24. 19. 33. 23. 36. 26. 8. 32. 26. 24. 13. 32. 23. 18. 18. 33. 23. 17.
9. 10. 32. 24. 1. 1. 1. 3. 2. 1. 2. 2. 1. 2. 1. 2. 3. 2.
1. 2. 2. 2. 1. 2. 1. 2. 2. 3. 2. 2. 2. 2. 1. 2. 2. 1.
3. 2. 2. 2. 3. 2. 2. 3. 2. 2. 2. 2. 2. 3. 2. 2. 2. 2.
1. 2. 1. 2. 2. 2. 2. 3. 2. 3. 2. 3. 2. 2. 2. 2. 1. 2.
2. 3. 3. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 3. 3. 2. 2. 2.
3. 2. 2. 2. 2. 2. 2. 2. 2. 2. 3. 2. 1. 2. 2. 2. 1. 2.
2. 3. 2. 2. 2. 2. 2. 3. 3. 2. 3. 2. 3. 2. 1. 2. 3. 2.
2. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 2. 2. 3. 2. 1. 2. 3.
3. 2. 2. 2. 3. 3. 2. 2. 3. 3. 2. 2. 3. 1. 2. 2. 3. 3.
2. 1. 2. 2. 3. 2. 2. 3. 2. 2. 2. 3. 1. 3. 2. 2. 2. 3.
2. 2. 2. 1. 2. 2. 1. 1. 1. 1. 1. 1.]
<class 'numpy.ndarray'>
float64
pore.volume
[ 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 542. 1619. 1180.
560. 2165. 2762. 1624. 495. 948. 668. 373. 254. 684. 1336. 412.
298. 1072. 245. 1185. 656. 1649. 2067. 548. 544. 402. 1346. 447.
856. 273. 577. 1011. 965. 757. 1617. 304. 330. 297. 430. 831.
1010. 1016. 486. 463. 294. 2124. 2968. 1700. 1130. 457. 316. 984.
716. 473. 294. 489. 729. 2570. 1027. 355. 2316. 1285. 406. 354.
488. 384. 617. 2158. 449. 387. 788. 350. 260. 272. 374. 269.
1447. 373. 589. 258. 1479. 595. 2225. 261. 366. 935. 573. 362.
304. 1968. 1536. 466. 1374. 568. 599. 520. 1770. 796. 731. 285.
232. 707. 2512. 1817. 1290. 1614. 1371. 142. 615.]
<class 'numpy.ndarray'>
float64
pore.surface_area
[ -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. 75. 164. 144.
90. 202. 195. 119. 90. 94. 101. 71. 57. 87. 127. 80. 57. 100.
47. 98. 102. 113. 177. 77. 69. 86. 109. 79. 111. 54. 79. 113.
104. 91. 176. 56. 52. 56. 62. 89. 101. 107. 68. 69. 60. 154.
211. 121. 92. 82. 60. 96. 103. 79. 62. 86. 80. 210. 100. 59.
158. 105. 63. 80. 50. 66. 87. 158. 80. 84. 104. 67. 57. 46.
67. 74. 150. 57. 46. 56. 141. 81. 168. 52. 87. 95. 66. 62.
87. 149. 147. 54. 99. 98. 66. 89. 127. 83. 71. 79. 54. 71.
183. 175. 179. 162. 157. 57. 124.]
<class 'numpy.ndarray'>
float64
throat.cross_sectional_area
[36. 33. 23. 37. 37. 18. 29. 24. 24. 15. 24. 38. 30. 23. 23. 29. 17. 44.
24. 24. 23. 28. 25. 16. 28. 23. 18. 23. 28. 23. 17. 24. 33. 20. 16. 23.
28. 18. 14. 17. 15. 38. 9. 19. 26. 18. 15. 22. 20. 17. 19. 22. 33. 18.
24. 24. 19. 25. 20. 14. 22. 21. 15. 17. 27. 13. 24. 11. 16. 30. 23. 23.
26. 24. 17. 25. 34. 20. 20. 18. 26. 17. 19. 15. 15. 25. 13. 19. 35. 23.
10. 20. 23. 16. 21. 8. 22. 17. 24. 20. 16. 21. 21. 14. 22. 16. 19. 19.
16. 37. 19. 23. 13. 26. 23. 19. 24. 27. 22. 20. 23. 29. 12. 24. 27. 13.
11. 22. 18. 23. 5. 24. 23. 30. 15. 19. 10. 23. 40. 26. 15. 30. 21. 25.
11. 23. 18. 15. 20. 12. 23. 23. 14. 22. 34. 23. 13. 34. 14. 24. 20. 35.
18. 39. 15. 20. 21. 21. 15. 23. 33. 20. 16. 27. 19. 25. 21. 23. 21. 16.
32. 27. 17. 17. 11. 20. 29. 10. 19. 22. 12. 37. 21. 17. 17. 13. 12. 24.
18. 25. 23. 34. 24. 11. 27. 13. 32. 20. 38. 29. 14. 11. 22. 11. 19. 26.
14. 23. 15. 18. 24. 12. 31. 33. 28. 19. 14. 18. 11. 18. 12. 33. 13. 26.
20. 25. 21. 19. 27. 19. 11. 17. 16. 29. 23. 15. 19. 14. 21. 29. 23. 14.
7. 19. 23. 14. 30. 25. 12. 18. 26. 36. 22. 24. 19. 27. 24. 14. 31. 23.
28. 14. 20. 30. 19. 26. 17. 7. 20. 3. 31. 37. 24. 12. 14. 21. 22. 23.
31. 26. 18. 17. 24. 21. 24. 23. 20. 9. 23. 21. 19. 26. 28. 21. 17. 11.
23. 21. 23. 14. 26. 31. 35. 28. 24. 26. 14. 15. 22. 18. 37. 20. 11. 18.
24. 19. 33. 23. 36. 26. 8. 32. 26. 24. 13. 32. 23. 18. 18. 33. 23. 17.
9. 10. 32. 24. 22. 4. 1. 8. 8. 10. 4. 6. 10. 6. 1. 5. 9. 6.
19. 19. 6. 13. 18. 28. 5. 8. 27. 7. 3. 7. 5. 10. 17. 20. 6. 9.
11. 25. 16. 5. 7. 35. 12. 5. 7. 28. 12. 7. 6. 7. 7. 13. 17. 6.
3. 20. 20. 7. 7. 7. 10. 9. 4. 10. 17. 6. 6. 15. 6. 11. 1. 14.
9. 11. 11. 15. 16. 8. 7. 13. 14. 4. 18. 15. 15. 7. 26. 7. 9. 11.
15. 8. 12. 29. 22. 6. 18. 3. 7. 24. 14. 15. 3. 6. 6. 22. 1. 23.
5. 10. 4. 13. 7. 9. 12. 23. 8. 17. 23. 16. 16. 12. 1. 21. 15. 8.
11. 11. 6. 24. 5. 15. 2. 6. 9. 5. 7. 11. 6. 6. 9. 1. 6. 5.
5. 15. 24. 23. 6. 6. 7. 15. 9. 25. 8. 6. 6. 7. 10. 27. 15. 12.
10. 2. 5. 23. 9. 14. 10. 25. 9. 10. 32. 10. 9. 20. 11. 4. 10. 32.
21. 27. 9. 1. 5. 23. 16. 25. 23. 5. 2. 4.]
<class 'numpy.ndarray'>
float64
throat.equivalent_diameter
[6.770275 6.48204481 5.41151638 6.86366252 6.86366252 4.78730736
6.07650778 5.52790639 5.52790639 4.37019372 5.52790639 6.95579634
6.18038723 5.41151638 5.41151638 6.07650778 4.65242649 7.48482064
5.52790639 5.52790639 5.41151638 5.97082132 5.64189584 4.51351667
5.97082132 5.41151638 4.78730736 5.41151638 5.97082132 5.41151638
4.65242649 5.52790639 6.48204481 5.04626504 4.51351667 5.41151638
5.97082132 4.78730736 4.22200825 4.65242649 4.37019372 6.95579634
3.3851375 4.91849076 5.75362739 4.78730736 4.37019372 5.29256743
5.04626504 4.65242649 4.91849076 5.29256743 6.48204481 4.78730736
5.52790639 5.52790639 4.91849076 5.64189584 5.04626504 4.22200825
5.29256743 5.17088295 4.37019372 4.65242649 5.86323014 4.06842895
5.52790639 3.74241032 4.51351667 6.18038723 5.41151638 5.41151638
5.75362739 5.52790639 4.65242649 5.64189584 6.57952464 5.04626504
5.04626504 4.78730736 5.75362739 4.65242649 4.91849076 4.37019372
4.37019372 5.64189584 4.06842895 4.91849076 6.67558118 5.41151638
3.56824823 5.04626504 5.41151638 4.51351667 5.17088295 3.19153824
5.29256743 4.65242649 5.52790639 5.04626504 4.51351667 5.17088295
5.17088295 4.22200825 5.29256743 4.51351667 4.91849076 4.91849076
4.51351667 6.86366252 4.91849076 5.41151638 4.06842895 5.75362739
5.41151638 4.91849076 5.52790639 5.86323014 5.29256743 5.04626504
5.41151638 6.07650778 3.9088201 5.52790639 5.86323014 4.06842895
3.74241032 5.29256743 4.78730736 5.41151638 2.52313252 5.52790639
5.41151638 6.18038723 4.37019372 4.91849076 3.56824823 5.41151638
7.13649646 5.75362739 4.37019372 6.18038723 5.17088295 5.64189584
3.74241032 5.41151638 4.78730736 4.37019372 5.04626504 3.9088201
5.41151638 5.41151638 4.22200825 5.29256743 6.57952464 5.41151638
4.06842895 6.57952464 4.22200825 5.52790639 5.04626504 6.67558118
4.78730736 7.04672564 4.37019372 5.04626504 5.17088295 5.17088295
4.37019372 5.41151638 6.48204481 5.04626504 4.51351667 5.86323014
4.91849076 5.64189584 5.17088295 5.41151638 5.17088295 4.51351667
6.38307649 5.86323014 4.65242649 4.65242649 3.74241032 5.04626504
6.07650778 3.56824823 4.91849076 5.29256743 3.9088201 6.86366252
5.17088295 4.65242649 4.65242649 4.06842895 3.9088201 5.52790639
4.78730736 5.64189584 5.41151638 6.57952464 5.52790639 3.74241032
5.86323014 4.06842895 6.38307649 5.04626504 6.95579634 6.07650778
4.22200825 3.74241032 5.29256743 3.74241032 4.91849076 5.75362739
4.22200825 5.41151638 4.37019372 4.78730736 5.52790639 3.9088201
6.28254931 6.48204481 5.97082132 4.91849076 4.22200825 4.78730736
3.74241032 4.78730736 3.9088201 6.48204481 4.06842895 5.75362739
5.04626504 5.64189584 5.17088295 4.91849076 5.86323014 4.91849076
3.74241032 4.65242649 4.51351667 6.07650778 5.41151638 4.37019372
4.91849076 4.22200825 5.17088295 6.07650778 5.41151638 4.22200825
2.98541066 4.91849076 5.41151638 4.22200825 6.18038723 5.64189584
3.9088201 4.78730736 5.75362739 6.770275 5.29256743 5.52790639
4.91849076 5.86323014 5.52790639 4.22200825 6.28254931 5.41151638
5.97082132 4.22200825 5.04626504 6.18038723 4.91849076 5.75362739
4.65242649 2.98541066 5.04626504 1.95441005 6.28254931 6.86366252
5.52790639 3.9088201 4.22200825 5.17088295 5.29256743 5.41151638
6.28254931 5.75362739 4.78730736 4.65242649 5.52790639 5.17088295
5.52790639 5.41151638 5.04626504 3.3851375 5.41151638 5.17088295
4.91849076 5.75362739 5.97082132 5.17088295 4.65242649 3.74241032
5.41151638 5.17088295 5.41151638 4.22200825 5.75362739 6.28254931
6.67558118 5.97082132 5.52790639 5.75362739 4.22200825 4.37019372
5.29256743 4.78730736 6.86366252 5.04626504 3.74241032 4.78730736
5.52790639 4.91849076 6.48204481 5.41151638 6.770275 5.75362739
3.19153824 6.38307649 5.75362739 5.52790639 4.06842895 6.38307649
5.41151638 4.78730736 4.78730736 6.48204481 5.41151638 4.65242649
3.3851375 3.56824823 6.38307649 5.52790639 5.29256743 2.25675833
1.12837917 3.19153824 3.19153824 3.56824823 2.25675833 2.7639532
3.56824823 2.7639532 1.12837917 2.52313252 3.3851375 2.7639532
4.91849076 4.91849076 2.7639532 4.06842895 4.78730736 5.97082132
2.52313252 3.19153824 5.86323014 2.98541066 1.95441005 2.98541066
2.52313252 3.56824823 4.65242649 5.04626504 2.7639532 3.3851375
3.74241032 5.64189584 4.51351667 2.52313252 2.98541066 6.67558118
3.9088201 2.52313252 2.98541066 5.97082132 3.9088201 2.98541066
2.7639532 2.98541066 2.98541066 4.06842895 4.65242649 2.7639532
1.95441005 5.04626504 5.04626504 2.98541066 2.98541066 2.98541066
3.56824823 3.3851375 2.25675833 3.56824823 4.65242649 2.7639532
2.7639532 4.37019372 2.7639532 3.74241032 1.12837917 4.22200825
3.3851375 3.74241032 3.74241032 4.37019372 4.51351667 3.19153824
2.98541066 4.06842895 4.22200825 2.25675833 4.78730736 4.37019372
4.37019372 2.98541066 5.75362739 2.98541066 3.3851375 3.74241032
4.37019372 3.19153824 3.9088201 6.07650778 5.29256743 2.7639532
4.78730736 1.95441005 2.98541066 5.52790639 4.22200825 4.37019372
1.95441005 2.7639532 2.7639532 5.29256743 1.12837917 5.41151638
2.52313252 3.56824823 2.25675833 4.06842895 2.98541066 3.3851375
3.9088201 5.41151638 3.19153824 4.65242649 5.41151638 4.51351667
4.51351667 3.9088201 1.12837917 5.17088295 4.37019372 3.19153824
3.74241032 3.74241032 2.7639532 5.52790639 2.52313252 4.37019372
1.59576912 2.7639532 3.3851375 2.52313252 2.98541066 3.74241032
2.7639532 2.7639532 3.3851375 1.12837917 2.7639532 2.52313252
2.52313252 4.37019372 5.52790639 5.41151638 2.7639532 2.7639532
2.98541066 4.37019372 3.3851375 5.64189584 3.19153824 2.7639532
2.7639532 2.98541066 3.56824823 5.86323014 4.37019372 3.9088201
3.56824823 1.59576912 2.52313252 5.41151638 3.3851375 4.22200825
3.56824823 5.64189584 3.3851375 3.56824823 6.38307649 3.56824823
3.3851375 5.04626504 3.74241032 2.25675833 3.56824823 6.38307649
5.17088295 5.86323014 3.3851375 1.12837917 2.52313252 5.41151638
4.51351667 5.64189584 5.41151638 2.52313252 1.59576912 2.25675833]
<class 'numpy.ndarray'>
float64
══════════════════════════════════════════════════════════════════════════════
net : <openpnm.network.Network at 0x18f436b9860>
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
# Properties Valid Values
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
2 throat.conns 534 / 534
3 pore.coords 189 / 189
4 pore.region_label 189 / 189
5 pore.phase 189 / 189
6 throat.phases 534 / 534
7 pore.region_volume 189 / 189
8 pore.equivalent_diameter 189 / 189
9 pore.local_peak 189 / 189
10 pore.global_peak 189 / 189
11 pore.geometric_centroid 189 / 189
12 throat.global_peak 534 / 534
13 pore.inscribed_diameter 189 / 189
14 pore.extended_diameter 189 / 189
15 throat.inscribed_diameter 534 / 534
16 throat.total_length 534 / 534
17 throat.direct_length 534 / 534
18 throat.perimeter 534 / 534
19 pore.volume 189 / 189
20 pore.surface_area 189 / 189
21 throat.cross_sectional_area 534 / 534
22 throat.equivalent_diameter 534 / 534
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
# Labels Assigned Locations
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
2 pore.all 189
3 throat.all 534
4 pore.phase1 81
5 throat.phase1_phase2 346
6 pore.phase2 108
7 throat.phase2_phase1 346
8 throat.phase2_phase2 188
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
ax = op.visualization.plot_connections(pn2, throats=pn2['throat.phase2_phase2'], c='k')
ax = op.visualization.plot_connections(pn2, throats=pn2['throat.phase2_phase1'], c='grey', ax=ax)
ax = op.visualization.plot_coordinates(pn2, pores=pn2['pore.phase2'], c='r', markersize=50, ax=ax)
ax = op.visualization.plot_coordinates(pn2, pores=pn2['pore.phase1'], c='g', markersize=50, ax=ax)
fig, ax = plt.gcf(), plt.gca()
ax.imshow(net2.regions.T)
ax.axis(False);
Now can see the particles are indicated by a green marker, the void pores by a red marker, the solid-void interconnections are in grey, and the void-void throats are black.
phase_alias#
In the previous section the default phase names created by snow2 were the uncreative “phase1” and “phase2”. The snow2 function allows for these to be given more desriptive names. This is done by supplying a dictionary with the voxels value as the key and the desired phase name as the value.
net3 = ps.networks.snow2(phases=im.astype(int) + 1, phase_alias={1: 'solid', 2: 'void'}, boundary_width=0)
pn3 = op.io.network_from_porespy(net3.network)
print(pn3)
throat.conns
[[ 0 82]
[ 0 83]
[ 0 90]
...
[183 187]
[184 188]
[186 188]]
<class 'numpy.ndarray'>
int32
pore.coords
[[ 16. 80. 0. ]
[ 16. 251. 0. ]
[ 25. 144. 0. ]
[ 25. 181. 0. ]
[ 33. 379. 0. ]
[ 34. 320. 0. ]
[ 37. 19. 0. ]
[ 40. 109. 0. ]
[ 49. 58. 0. ]
[ 53. 234. 0. ]
[ 59. 197. 0. ]
[ 61. 272. 0. ]
[ 64. 139. 0. ]
[ 71. 316. 0. ]
[ 72. 87. 0. ]
[ 74. 24. 0. ]
[ 74. 367. 0. ]
[ 89. 225. 0. ]
[ 95. 57. 0. ]
[107. 151. 0. ]
[108. 327. 0. ]
[111. 18. 0. ]
[111. 113. 0. ]
[118. 189. 0. ]
[124. 255. 0. ]
[125. 364. 0. ]
[126. 293. 0. ]
[128. 78. 0. ]
[143. 218. 0. ]
[144. 152. 0. ]
[148. 329. 0. ]
[151. 47. 0. ]
[157. 116. 0. ]
[165. 294. 0. ]
[169. 370. 0. ]
[171. 256. 0. ]
[173. 177. 0. ]
[185. 16. 0. ]
[189. 54. 0. ]
[198. 347. 0. ]
[202. 298. 0. ]
[206. 91. 0. ]
[206. 228. 0. ]
[215. 174. 0. ]
[215. 381. 0. ]
[221. 135. 0. ]
[226. 261. 0. ]
[238. 16. 0. ]
[240. 306. 0. ]
[242. 80. 0. ]
[242. 346. 0. ]
[258. 383. 0. ]
[262. 244. 0. ]
[263. 154. 0. ]
[263. 196. 0. ]
[264. 49. 0. ]
[272. 118. 0. ]
[279. 350. 0. ]
[282. 310. 0. ]
[284. 17. 0. ]
[284. 82. 0. ]
[298. 257. 0. ]
[298. 383. 0. ]
[300. 190. 0. ]
[313. 333. 0. ]
[315. 224. 0. ]
[318. 154. 0. ]
[319. 68. 0. ]
[322. 22. 0. ]
[324. 292. 0. ]
[339. 103. 0. ]
[339. 382. 0. ]
[351. 214. 0. ]
[359. 173. 0. ]
[360. 351. 0. ]
[361. 309. 0. ]
[363. 24. 0. ]
[368. 251. 0. ]
[379. 383. 0. ]
[380. 115. 0. ]
[382. 61. 0. ]
[ 13.6402214 8.38929889 0. ]
[ 16.95243978 45.06670784 0. ]
[ 11.97881356 114.99661017 0. ]
[ 7.94285714 162.5 0. ]
[ 21.47852194 213.90808314 0. ]
[ 26.96234613 289.51737871 0. ]
[ 14.15455665 348.89593596 0. ]
[ 12.02626263 390.41616162 0. ]
[ 47.01476793 165.32067511 0. ]
[ 44.01197605 83.39221557 0. ]
[ 41.99463807 252.90884718 0. ]
[ 42.9488189 131.06692913 0. ]
[ 56.65789474 389.17251462 0. ]
[ 52.03517964 346.89296407 0. ]
[ 57.24271845 6.6092233 0. ]
[ 53.36577181 34.5704698 0. ]
[ 75.50932836 112.99813433 0. ]
[ 67.55102041 217.95510204 0. ]
[ 85.64050633 250.21772152 0. ]
[ 72.25609756 54.96493902 0. ]
[ 83.83201941 171.28562765 0. ]
[ 94.43589744 288.27672956 0. ]
[ 89.02554745 202.08394161 0. ]
[ 83.51102941 338.70220588 0. ]
[ 89.7238806 6.6318408 0. ]
[100.17904903 385.71768202 0. ]
[ 91.40268456 133.92170022 0. ]
[100.8411215 85.18457944 0. ]
[ 94.01831502 33.63003663 0. ]
[100.89081456 353.32582322 0. ]
[116.80811078 222.5776459 0. ]
[121.77202073 47.80103627 0. ]
[130.32232497 130.89035667 0. ]
[147.36301793 15.2436611 0. ]
[123.51973684 165.34210526 0. ]
[126.82727273 340.2 0. ]
[127.93602694 316.003367 0. ]
[133.21162791 102.63023256 0. ]
[146.82551143 272.91576414 0. ]
[145.75247525 386.81287129 0. ]
[145.1476378 184.75885827 0. ]
[146.84773663 243.35185185 0. ]
[147.79049676 354.16414687 0. ]
[145.69387755 305.51360544 0. ]
[167.09887006 81.39500942 0. ]
[186.70990566 137.57985175 0. ]
[174.02823529 217.22176471 0. ]
[179.37522124 320.02743363 0. ]
[171.56455142 346.64770241 0. ]
[174.16455696 38.11075949 0. ]
[193.08434959 274.45934959 0. ]
[188.18994413 389.81564246 0. ]
[199.50105708 250.02536998 0. ]
[193.84693878 367.58843537 0. ]
[211.44580777 6.73619632 0. ]
[198.25240055 196.12482853 0. ]
[221.12957198 47.73307393 0. ]
[218.59006816 325.37877313 0. ]
[219.4 357.54647887 0. ]
[234.84110535 215.86183074 0. ]
[237.01089494 108.41400778 0. ]
[223.16995074 287. 0. ]
[235.30508475 392.88418079 0. ]
[235.20491803 154.69262295 0. ]
[237.8125 369.94270833 0. ]
[244.94165316 174.69854133 0. ]
[262.79564411 277.99258573 0. ]
[249.28730512 134.50556793 0. ]
[261.64082687 6.20155039 0. ]
[260.71827411 326.93527919 0. ]
[261.25428571 26.4 0. ]
[259.54230769 360.39230769 0. ]
[263.35294118 70.85661765 0. ]
[264.55882353 93.45454545 0. ]
[278. 393.32713755 0. ]
[284.98479613 221.96406358 0. ]
[275.91420912 178.3538874 0. ]
[287.68421053 143.06791171 0. ]
[278.40310078 372.10077519 0. ]
[296.35091278 47.40162272 0. ]
[291.95294118 165.0907563 0. ]
[307.04719101 111.03505618 0. ]
[291.01532567 331.02681992 0. ]
[305.61748634 6.22131148 0. ]
[310.40641711 360.84278075 0. ]
[300.36998255 285.69458988 0. ]
[306.24585635 310.7320442 0. ]
[319.15789474 393.06578947 0. ]
[333.37347561 252.06097561 0. ]
[330.06184896 188.7890625 0. ]
[333.86480687 312.37339056 0. ]
[345.93449782 46.92212518 0. ]
[343.50704225 7.79225352 0. ]
[342.4457429 330.89983306 0. ]
[335.88076923 355.18461538 0. ]
[349.14293785 137.18587571 0. ]
[348.64447236 75.91331658 0. ]
[351.80164159 282.27770178 0. ]
[358.29824561 393.44210526 0. ]
[359.07758621 372.67241379 0. ]
[367.0311174 91.54879774 0. ]
[382.17356688 210.19785032 0. ]
[385.22014309 340.11172262 0. ]
[386.34341085 22.78682171 0. ]
[384.42998761 281.366171 0. ]
[385.4726477 149.26185266 0. ]
[394.28873239 393.14788732 0. ]
[391.6601626 89.10243902 0. ]]
<class 'numpy.ndarray'>
float64
pore.region_label
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108
109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126
127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144
145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162
163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180
181 182 183 184 185 186 187 188 189]
<class 'numpy.ndarray'>
int32
pore.phase
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2]
<class 'numpy.ndarray'>
int32
throat.phases
[[1 2]
[1 2]
[1 2]
...
[2 2]
[2 2]
[2 2]]
<class 'numpy.ndarray'>
int32
pore.region_volume
[ 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 542. 1619. 1180.
560. 2165. 2762. 1624. 495. 948. 668. 373. 254. 684. 1336. 412.
298. 1072. 245. 1185. 656. 1649. 2067. 548. 544. 402. 1346. 447.
856. 273. 577. 1011. 965. 757. 1617. 304. 330. 297. 430. 831.
1010. 1016. 486. 463. 294. 2124. 2968. 1700. 1130. 457. 316. 984.
716. 473. 294. 489. 729. 2570. 1027. 355. 2316. 1285. 406. 354.
488. 384. 617. 2158. 449. 387. 788. 350. 260. 272. 374. 269.
1447. 373. 589. 258. 1479. 595. 2225. 261. 366. 935. 573. 362.
304. 1968. 1536. 466. 1374. 568. 599. 520. 1770. 796. 731. 285.
232. 707. 2512. 1817. 1290. 1614. 1371. 142. 615.]
<class 'numpy.ndarray'>
float64
pore.equivalent_diameter
[31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 31.77544585 31.77544585 31.77544585
31.77544585 31.77544585 31.77544585 26.26967516 45.40236583 38.76109729
26.70232471 52.50298672 59.30166627 45.47242044 25.10485162 34.74235295
29.16374489 21.79262146 17.98340469 29.51094456 41.24376355 22.90359562
19.47884453 36.94472617 17.66192765 38.84313145 28.90060798 45.82108695
51.30093702 26.41467907 26.31809857 22.62393195 41.39783119 23.85661494
33.01352829 18.6438836 27.10459772 35.87819923 35.05247724 31.04581027
45.3743137 19.67396304 20.49802551 19.44613444 23.39856842 32.52786593
35.86045092 35.96680939 24.87557876 24.27982515 19.34767237 52.00346905
61.47336796 46.52426492 37.93099901 24.12199146 20.05850683 35.3958714
30.19336871 24.5406256 19.34767237 24.95223712 30.46623751 57.20337079
36.16098744 21.26029253 54.30306424 40.44889139 22.73621022 21.23032734
24.92671053 22.11162557 28.02835705 52.41804019 23.90992588 22.19783106
31.67511265 21.11004123 18.19456737 18.60970597 21.82181454 18.50679436
42.92292652 21.79262146 27.38499757 18.12445317 43.3949454 27.52412631
53.22553886 18.22952334 21.58716455 34.50331831 27.01048424 21.46887783
19.67396304 50.05732138 44.22325113 24.35835848 41.82620153 26.89237924
27.61648941 25.73100393 47.47245511 31.83549399 30.50800071 19.0492328
17.18695943 30.00300582 56.55420176 48.09860968 40.52750933 45.33220296
41.78051479 13.44618962 27.98289335]
<class 'numpy.ndarray'>
float64
pore.local_peak
[[ 17. 81.]
[ 17. 252.]
[ 26. 145.]
[ 26. 182.]
[ 34. 380.]
[ 35. 321.]
[ 38. 20.]
[ 41. 110.]
[ 50. 59.]
[ 54. 235.]
[ 60. 198.]
[ 62. 273.]
[ 65. 140.]
[ 72. 317.]
[ 73. 88.]
[ 75. 25.]
[ 75. 368.]
[ 90. 226.]
[ 96. 58.]
[108. 152.]
[109. 328.]
[112. 19.]
[112. 114.]
[119. 190.]
[125. 256.]
[126. 365.]
[127. 294.]
[129. 79.]
[144. 219.]
[145. 153.]
[149. 330.]
[152. 48.]
[158. 117.]
[166. 295.]
[170. 371.]
[172. 257.]
[174. 178.]
[186. 17.]
[190. 55.]
[199. 348.]
[203. 299.]
[207. 92.]
[207. 229.]
[216. 175.]
[216. 382.]
[222. 136.]
[227. 262.]
[239. 17.]
[241. 307.]
[243. 81.]
[243. 347.]
[259. 384.]
[263. 245.]
[264. 155.]
[264. 197.]
[265. 50.]
[273. 119.]
[280. 351.]
[283. 311.]
[285. 18.]
[285. 83.]
[299. 258.]
[299. 384.]
[301. 191.]
[314. 334.]
[316. 225.]
[319. 155.]
[320. 69.]
[323. 23.]
[325. 293.]
[340. 104.]
[340. 383.]
[352. 215.]
[360. 174.]
[361. 352.]
[362. 310.]
[364. 25.]
[369. 252.]
[380. 384.]
[381. 116.]
[383. 62.]
[ 10. 10.]
[ 18. 48.]
[ 13. 109.]
[ 9. 163.]
[ 20. 217.]
[ 21. 288.]
[ 18. 350.]
[ 10. 390.]
[ 49. 164.]
[ 43. 84.]
[ 40. 254.]
[ 44. 132.]
[ 59. 390.]
[ 51. 348.]
[ 59. 8.]
[ 55. 36.]
[ 83. 115.]
[ 69. 218.]
[ 82. 253.]
[ 73. 49.]
[ 80. 171.]
[ 93. 289.]
[ 94. 202.]
[ 84. 341.]
[ 91. 8.]
[102. 385.]
[ 89. 136.]
[101. 86.]
[ 96. 35.]
[101. 355.]
[118. 229.]
[123. 46.]
[134. 129.]
[144. 17.]
[125. 167.]
[128. 342.]
[129. 317.]
[135. 104.]
[147. 274.]
[145. 387.]
[147. 188.]
[149. 245.]
[150. 355.]
[146. 307.]
[166. 82.]
[185. 142.]
[176. 219.]
[180. 323.]
[168. 346.]
[174. 38.]
[196. 272.]
[190. 389.]
[196. 251.]
[192. 370.]
[210. 9.]
[200. 197.]
[225. 50.]
[217. 325.]
[221. 358.]
[231. 205.]
[242. 112.]
[225. 287.]
[237. 393.]
[239. 155.]
[238. 371.]
[244. 176.]
[265. 280.]
[248. 136.]
[262. 9.]
[260. 326.]
[262. 26.]
[260. 362.]
[264. 72.]
[264. 94.]
[279. 394.]
[285. 221.]
[274. 176.]
[288. 145.]
[279. 373.]
[296. 48.]
[291. 166.]
[308. 119.]
[292. 332.]
[306. 8.]
[315. 361.]
[300. 289.]
[307. 310.]
[320. 394.]
[334. 256.]
[332. 189.]
[337. 314.]
[345. 50.]
[344. 9.]
[342. 333.]
[336. 353.]
[351. 138.]
[350. 78.]
[352. 284.]
[360. 394.]
[360. 374.]
[370. 91.]
[383. 199.]
[385. 331.]
[389. 12.]
[383. 283.]
[385. 150.]
[396. 396.]
[391. 87.]]
<class 'numpy.ndarray'>
float64
pore.global_peak
[[ 16. 80.]
[ 16. 251.]
[ 25. 144.]
[ 25. 181.]
[ 33. 379.]
[ 34. 320.]
[ 37. 19.]
[ 40. 109.]
[ 49. 58.]
[ 53. 234.]
[ 59. 197.]
[ 61. 272.]
[ 64. 139.]
[ 71. 316.]
[ 72. 87.]
[ 74. 24.]
[ 74. 367.]
[ 89. 225.]
[ 95. 57.]
[107. 151.]
[108. 327.]
[111. 18.]
[111. 113.]
[118. 189.]
[124. 255.]
[125. 364.]
[126. 293.]
[128. 78.]
[143. 218.]
[144. 152.]
[148. 329.]
[151. 47.]
[157. 116.]
[165. 294.]
[169. 370.]
[171. 256.]
[173. 177.]
[185. 16.]
[189. 54.]
[198. 347.]
[202. 298.]
[206. 91.]
[206. 228.]
[215. 174.]
[215. 381.]
[221. 135.]
[226. 261.]
[238. 16.]
[240. 306.]
[242. 80.]
[242. 346.]
[258. 383.]
[262. 244.]
[263. 154.]
[263. 196.]
[264. 49.]
[272. 118.]
[279. 350.]
[282. 310.]
[284. 17.]
[284. 82.]
[298. 257.]
[298. 383.]
[300. 190.]
[313. 333.]
[315. 224.]
[318. 154.]
[319. 68.]
[322. 22.]
[324. 292.]
[339. 103.]
[339. 382.]
[351. 214.]
[359. 173.]
[360. 351.]
[361. 309.]
[363. 24.]
[368. 251.]
[379. 383.]
[380. 115.]
[382. 61.]
[ 0. 0.]
[ 0. 40.]
[ 0. 115.]
[ 25. 144.]
[ 0. 213.]
[ 0. 292.]
[ 0. 349.]
[ 0. 399.]
[ 25. 144.]
[ 42. 83.]
[ 41. 256.]
[ 31. 143.]
[ 61. 399.]
[ 46. 350.]
[ 37. 19.]
[ 42. 20.]
[ 82. 115.]
[ 55. 230.]
[ 91. 258.]
[ 72. 48.]
[ 79. 170.]
[ 92. 288.]
[ 89. 195.]
[ 84. 341.]
[111. 18.]
[101. 399.]
[ 90. 130.]
[100. 85.]
[104. 20.]
[ 98. 353.]
[117. 228.]
[122. 45.]
[144. 152.]
[147. 0.]
[112. 150.]
[115. 327.]
[116. 325.]
[135. 103.]
[126. 293.]
[143. 399.]
[146. 187.]
[148. 244.]
[149. 354.]
[157. 292.]
[165. 81.]
[184. 141.]
[176. 211.]
[179. 322.]
[171. 343.]
[188. 51.]
[202. 297.]
[186. 399.]
[199. 255.]
[193. 371.]
[185. 16.]
[184. 206.]
[224. 49.]
[240. 306.]
[220. 357.]
[230. 204.]
[241. 111.]
[224. 286.]
[215. 381.]
[237. 157.]
[251. 382.]
[243. 175.]
[264. 279.]
[248. 131.]
[238. 16.]
[242. 346.]
[261. 25.]
[249. 347.]
[251. 78.]
[278. 81.]
[258. 383.]
[262. 244.]
[263. 194.]
[301. 129.]
[290. 381.]
[295. 47.]
[290. 163.]
[307. 119.]
[280. 343.]
[284. 17.]
[298. 383.]
[296. 285.]
[306. 309.]
[298. 383.]
[333. 255.]
[331. 188.]
[335. 317.]
[349. 54.]
[322. 22.]
[341. 329.]
[332. 354.]
[351. 137.]
[351. 72.]
[337. 262.]
[339. 382.]
[348. 380.]
[351. 72.]
[399. 202.]
[399. 331.]
[399. 0.]
[399. 284.]
[399. 155.]
[379. 383.]
[399. 89.]]
<class 'numpy.ndarray'>
float64
pore.geometric_centroid
[[ 16. 80. ]
[ 16. 251. ]
[ 25. 144. ]
[ 25. 181. ]
[ 33. 379. ]
[ 34. 320. ]
[ 37. 19. ]
[ 40. 109. ]
[ 49. 58. ]
[ 53. 234. ]
[ 59. 197. ]
[ 61. 272. ]
[ 64. 139. ]
[ 71. 316. ]
[ 72. 87. ]
[ 74. 24. ]
[ 74. 367. ]
[ 89. 225. ]
[ 95. 57. ]
[107. 151. ]
[108. 327. ]
[111. 18. ]
[111. 113. ]
[118. 189. ]
[124. 255. ]
[125. 364. ]
[126. 293. ]
[128. 78. ]
[143. 218. ]
[144. 152. ]
[148. 329. ]
[151. 47. ]
[157. 116. ]
[165. 294. ]
[169. 370. ]
[171. 256. ]
[173. 177. ]
[185. 16. ]
[189. 54. ]
[198. 347. ]
[202. 298. ]
[206. 91. ]
[206. 228. ]
[215. 174. ]
[215. 381. ]
[221. 135. ]
[226. 261. ]
[238. 16. ]
[240. 306. ]
[242. 80. ]
[242. 346. ]
[258. 383. ]
[262. 244. ]
[263. 154. ]
[263. 196. ]
[264. 49. ]
[272. 118. ]
[279. 350. ]
[282. 310. ]
[284. 17. ]
[284. 82. ]
[298. 257. ]
[298. 383. ]
[300. 190. ]
[313. 333. ]
[315. 224. ]
[318. 154. ]
[319. 68. ]
[322. 22. ]
[324. 292. ]
[339. 103. ]
[339. 382. ]
[351. 214. ]
[359. 173. ]
[360. 351. ]
[361. 309. ]
[363. 24. ]
[368. 251. ]
[379. 383. ]
[380. 115. ]
[382. 61. ]
[ 13.6402214 8.38929889]
[ 16.95243978 45.06670784]
[ 11.97881356 114.99661017]
[ 7.94285714 162.5 ]
[ 21.47852194 213.90808314]
[ 26.96234613 289.51737871]
[ 14.15455665 348.89593596]
[ 12.02626263 390.41616162]
[ 47.01476793 165.32067511]
[ 44.01197605 83.39221557]
[ 41.99463807 252.90884718]
[ 42.9488189 131.06692913]
[ 56.65789474 389.17251462]
[ 52.03517964 346.89296407]
[ 57.24271845 6.6092233 ]
[ 53.36577181 34.5704698 ]
[ 75.50932836 112.99813433]
[ 67.55102041 217.95510204]
[ 85.64050633 250.21772152]
[ 72.25609756 54.96493902]
[ 83.83201941 171.28562765]
[ 94.43589744 288.27672956]
[ 89.02554745 202.08394161]
[ 83.51102941 338.70220588]
[ 89.7238806 6.6318408 ]
[100.17904903 385.71768202]
[ 91.40268456 133.92170022]
[100.8411215 85.18457944]
[ 94.01831502 33.63003663]
[100.89081456 353.32582322]
[116.80811078 222.5776459 ]
[121.77202073 47.80103627]
[130.32232497 130.89035667]
[147.36301793 15.2436611 ]
[123.51973684 165.34210526]
[126.82727273 340.2 ]
[127.93602694 316.003367 ]
[133.21162791 102.63023256]
[146.82551143 272.91576414]
[145.75247525 386.81287129]
[145.1476378 184.75885827]
[146.84773663 243.35185185]
[147.79049676 354.16414687]
[145.69387755 305.51360544]
[167.09887006 81.39500942]
[186.70990566 137.57985175]
[174.02823529 217.22176471]
[179.37522124 320.02743363]
[171.56455142 346.64770241]
[174.16455696 38.11075949]
[193.08434959 274.45934959]
[188.18994413 389.81564246]
[199.50105708 250.02536998]
[193.84693878 367.58843537]
[211.44580777 6.73619632]
[198.25240055 196.12482853]
[221.12957198 47.73307393]
[218.59006816 325.37877313]
[219.4 357.54647887]
[234.84110535 215.86183074]
[237.01089494 108.41400778]
[223.16995074 287. ]
[235.30508475 392.88418079]
[235.20491803 154.69262295]
[237.8125 369.94270833]
[244.94165316 174.69854133]
[262.79564411 277.99258573]
[249.28730512 134.50556793]
[261.64082687 6.20155039]
[260.71827411 326.93527919]
[261.25428571 26.4 ]
[259.54230769 360.39230769]
[263.35294118 70.85661765]
[264.55882353 93.45454545]
[278. 393.32713755]
[284.98479613 221.96406358]
[275.91420912 178.3538874 ]
[287.68421053 143.06791171]
[278.40310078 372.10077519]
[296.35091278 47.40162272]
[291.95294118 165.0907563 ]
[307.04719101 111.03505618]
[291.01532567 331.02681992]
[305.61748634 6.22131148]
[310.40641711 360.84278075]
[300.36998255 285.69458988]
[306.24585635 310.7320442 ]
[319.15789474 393.06578947]
[333.37347561 252.06097561]
[330.06184896 188.7890625 ]
[333.86480687 312.37339056]
[345.93449782 46.92212518]
[343.50704225 7.79225352]
[342.4457429 330.89983306]
[335.88076923 355.18461538]
[349.14293785 137.18587571]
[348.64447236 75.91331658]
[351.80164159 282.27770178]
[358.29824561 393.44210526]
[359.07758621 372.67241379]
[367.0311174 91.54879774]
[382.17356688 210.19785032]
[385.22014309 340.11172262]
[386.34341085 22.78682171]
[384.42998761 281.366171 ]
[385.4726477 149.26185266]
[394.28873239 393.14788732]
[391.6601626 89.10243902]]
<class 'numpy.ndarray'>
float64
throat.global_peak
[[ 0. 75. 0.]
[ 0. 81. 0.]
[ 27. 92. 0.]
...
[399. 383. 0.]
[399. 62. 0.]
[399. 115. 0.]]
<class 'numpy.ndarray'>
float64
pore.inscribed_diameter
[32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 20. 36. 26.
18. 40. 40.2492218 34.05877304 20. 26.07680893
20.39607811 15.62049961 12.80624866 22. 31.1126976 15.62049961
14.42220497 26. 12.64911079 24.73863411 17.88854408 35.6089859
38. 18. 20.88061333 15.62049961 31.1126976 18.
26. 14.14213562 22.36067963 24.16609192 26.83281517 21.54065895
32.55764008 14.14213562 15.62049961 14.42220497 18.86796188 25.45584488
26.90724754 26. 20.39607811 19.79899025 14.42220497 40.44749832
42.42640686 33.10589218 31.24099922 18. 15.62049961 24.33105087
22.36067963 17.88854408 14. 18. 22. 40.
26.90724754 17.08800697 35.77708817 31.1126976 18.86796188 16.
19.79899025 17.88854408 22. 40. 18.11077118 17.08800697
22.62741661 17.08800697 14. 14. 16.12451553 13.41640759
32. 15.2315464 18.97366524 14. 32. 22.09072113
39.39543152 13.41640759 14.14213562 24. 20. 17.88854408
14. 40. 32. 16.4924221 31.24099922 18.
22. 20. 39.84971619 24.08318901 24.16609192 13.41640759
12.64911079 23.32380676 36. 31.1126976 24. 36.
32. 8.48528099 20. ]
<class 'numpy.ndarray'>
float64
pore.extended_diameter
[32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 32. 32. 32.
32. 32. 32. 51.88448715 53.66563034 45.25483322
32. 49.67897034 56.46237564 58. 45.65084839 32.
20.39607811 18.86796188 20. 37.20215225 32.24903107 32.
22. 27.85677719 23.32380676 34.92849731 17.88854408 35.6089859
38. 28.07133675 24.16609192 32. 52.34500885 22.62741661
26. 17.88854408 24.16609192 24.16609192 26.83281517 32.
49.1934967 22. 18. 16. 19.69771576 32.
46.69047165 26. 20.59126091 19.79899025 16. 40.44749832
42.42640686 36.22154236 31.24099922 22.36067963 26. 30.
35.77708817 24.08318901 17.08800697 32. 30.4630928 40.
32. 17.08800697 35.77708817 31.1126976 18.86796188 32.
22. 18. 26. 40. 23.32380676 32.
32. 17.08800697 18. 14. 20. 32.
32. 28. 28.84440994 16. 32. 25.29822159
40. 18. 32. 32. 26. 18.
32. 40. 32. 22.80350876 34.92849731 32.
25.45584488 25.45584488 40.49691391 34. 34. 32.
14. 34. 67.20118713 56.35601044 54.91812134 59.36328888
56.35601044 32. 32.80244064]
<class 'numpy.ndarray'>
float64
throat.inscribed_diameter
[ 2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 2. 2.
2. 2. 2. 2. 44. 8.
2. 7.21110249 8.24621105 20. 5.65685415 5.65685415
20. 6. 2. 6.3245554 8.24621105 6.
38. 17.88854408 6. 14. 36. 28.
10. 8. 28. 7.21110249 5.65685415 8.
7.21110249 10.19803905 34. 20. 6. 18.
10. 21.54065895 14.42220497 6. 8.48528099 32.98484421
14.14213562 5.65685415 7.21110249 28. 12.16552544 8.
6. 6.3245554 8. 14.14213562 19.79899025 6.
6. 20. 40. 8. 7.21110249 7.21110249
10. 8.24621105 5.65685415 10. 17.20465088 5.65685415
6. 16. 6. 14.14213562 2. 12.80624866
10. 8.94427204 10. 15.62049961 16. 8.
8. 14. 28. 5.65685415 18.43908882 14.42220497
14.42220497 6.3245554 23.32380676 8. 8.94427204 12.
14.14213562 8. 12.80624866 27.78488731 20.88061333 6.
18. 5.65685415 8. 24. 11.66190338 16.
6. 6.3245554 5.65685415 22. 2. 24.
6. 10. 5.65685415 14. 8. 10.
11.31370831 21.54065895 8.24621105 18. 20.88061333 16.97056198
14.56021976 12. 2. 19.69771576 13.41640759 8.24621105
12. 12. 6. 22.80350876 6. 16.
4. 6. 10. 5.65685415 7.21110249 12.
6.3245554 6.3245554 10. 2. 6. 4.47213602
4.47213602 19.79899025 24. 25.61249733 6.3245554 5.65685415
8. 16. 8.94427204 22.36067963 8.24621105 5.65685415
5.65685415 14. 10. 23.32380676 14.42220497 11.31370831
10. 4. 6. 28.28427124 8.24621105 12.64911079
10. 21.54065895 8.94427204 10. 32. 10.
18. 17.88854408 12. 4.47213602 10.19803905 29.73213768
28.28427124 28. 10. 2. 5.65685415 24.
32. 50. 46. 10. 4. 8. ]
<class 'numpy.ndarray'>
float64
throat.total_length
[51.16344987 52.07648937 35.34453018 55.37934693 63.01655635 31.68268361
40.95057316 34.53017947 37.70908971 27.6951548 30.30438213 50.29255751
37.048434 42.02786372 28.45258244 40.36504811 40.2118794 43.77578561
45.15068695 36.25135831 26.01758366 41.42260757 36.56195864 26.53695198
33.05521097 35.2504025 28.75624347 42.06131525 34.6644879 32.28830769
28.71778592 35.67637163 38.4121247 27.43693363 27.82992826 44.40441842
47.47360858 39.41195917 27.78114742 40.17455455 35.25038109 45.61421233
26.9812432 44.51766502 45.20029854 39.62029805 22.60405926 41.53485664
43.3615994 32.7806152 52.084621 45.16919715 47.52074199 29.35125565
28.8316495 37.85388258 36.91494164 38.31200851 29.17695096 29.52200712
37.38200174 31.78329119 25.60334376 32.496721 33.00502544 32.20890416
42.31973412 31.40785162 22.58310498 40.60710342 31.79407204 34.26415839
24.12994565 38.34461444 28.97577777 35.5007564 43.04504296 26.64893031
37.01251444 26.69578326 48.30869584 35.49875057 31.12360584 26.98130299
27.98425603 25.03293294 28.94695111 39.68118341 54.69965934 36.88437733
28.66875876 32.11659231 36.44127443 30.34461985 38.93805818 32.33080671
39.9810112 29.77490364 39.18124167 39.12360827 45.48080797 37.05318593
37.03795803 29.31988193 37.72535252 26.66028507 30.00310654 36.92560859
28.26628678 32.32961711 29.53291766 37.22222677 24.98785599 33.28529858
36.32667414 32.10496244 48.31868348 30.74897277 40.00776353 32.53284886
37.87877921 33.03922743 30.07425063 40.33074984 52.26755848 29.28252542
25.73311684 33.3002654 29.40738041 40.03426365 30.05432403 31.20713498
37.3626286 50.14877414 27.64115477 35.17583182 28.19597843 47.20046216
51.91859894 32.99361356 27.97887958 41.52746188 40.83563718 36.28513903
28.78614228 31.51625616 35.56560971 29.33439894 33.92350312 27.94131782
46.50902521 40.33410648 33.52814604 34.17761617 54.60249573 46.95693083
31.82356115 38.81226441 26.39091912 43.29023799 52.95440042 47.24137753
27.71439023 50.56093527 34.28154791 28.18670222 28.6688384 35.54586524
29.51525577 39.99265508 36.6110703 36.98084903 25.44877134 40.12258567
51.83851423 52.45192954 39.38729124 33.74790878 27.26824997 36.41834766
40.9149084 50.50134347 36.2632252 51.66673975 33.7987506 35.72831819
34.30526897 25.43935765 30.74526791 35.77017252 27.09147238 36.56158243
41.02947102 32.74482935 32.26330844 38.28457927 28.84295554 52.53051003
32.48832691 46.4151423 28.14598022 46.77661722 40.44070217 27.54908887
39.30221846 30.78763952 47.75267699 36.35773706 44.46154422 40.70352413
28.39133094 27.11918718 34.05264162 28.47261081 30.02794561 35.98624015
25.67488415 27.93812884 25.84353397 27.99182655 36.78897228 25.74613332
42.45149182 46.03313629 38.82954819 29.85999757 28.23530833 25.92236301
30.58236429 37.0891923 33.2320047 44.43884452 28.22970413 40.13739472
28.05860768 43.89155886 29.71359758 28.11057764 41.49225975 36.2980856
28.30054678 29.31928281 38.1648743 46.29353406 34.97130579 27.93669352
28.31527745 26.57183803 37.91605826 43.95989859 34.72803392 27.23727446
30.74429716 30.97394364 25.36893056 27.56998968 43.56681423 37.29957247
24.46606068 28.9524191 46.31071698 48.41571928 49.08056995 44.65905051
33.14626826 44.95866965 27.07473566 23.67236264 38.10091387 37.04444335
45.25962118 27.22970771 29.52149534 42.92186236 23.469616 38.66959078
28.70805375 33.28871986 35.86353336 31.8828829 31.0882636 46.01215928
45.34596335 32.25923155 30.2708387 47.24380038 45.0150486 37.88543147
33.71946151 52.71661009 41.57081177 36.69357376 45.17539865 27.54852832
42.51392143 36.61643158 24.50393712 27.0743418 50.85724729 32.2578611
32.13203474 37.36414207 45.63440737 39.42220265 32.31628637 37.24851443
27.71381533 33.05982608 35.82918778 27.12709318 49.86401668 37.56851857
46.2781622 41.24939513 43.77560762 49.95974192 36.06478808 28.29863549
29.02189094 27.78393331 40.78490694 30.69525457 28.73167147 35.0045701
44.54784566 39.13906454 38.94687599 28.50248965 42.82446691 36.35087829
36.24511009 50.90989023 40.443077 27.45181456 23.37883157 49.29581039
31.47191565 47.74376044 33.1290575 42.69702152 30.57772359 38.78650096
37.32974579 35.24747702 43.30240715 32.15908664 48.173627 46.11490109
75.77670197 46.9371852 37.90751594 51.51278023 45.61789792 35.0234697
59.51927028 39.33957467 89.87839487 56.47746609 44.40401066 46.30011284
72.87241622 39.58148304 66.57255541 68.30031538 49.8476002 38.17698816
48.28017588 34.49822249 37.30074801 43.50517856 40.87218884 43.78580622
37.43956576 42.70588395 49.28888311 32.55449392 28.2330024 35.07877927
28.09164828 26.65114724 38.25035719 37.4909524 27.22400938 39.94328414
43.67105782 42.07911371 30.69707691 31.24234254 38.70037217 40.70111835
51.70536503 43.6582874 55.49642974 35.92784065 23.17229422 27.33966858
61.71464966 32.56734459 52.24651695 39.04893539 42.8782133 36.78280249
31.16497168 29.09484118 47.3179675 36.7724061 41.58822038 56.55871733
35.22033335 28.68317273 56.79360078 35.26311872 67.8970308 29.11381245
24.24881097 25.21476499 20.68876479 40.00223479 29.56575712 32.69985647
46.3626416 32.71227935 47.52285265 63.43187805 43.48053753 38.29176275
25.12470472 36.89260742 60.98306175 44.12628991 65.82180453 59.67485934
59.96020785 53.02011347 42.16681978 32.31091607 27.884307 48.17114281
39.57953312 30.59379948 49.67309163 25.29238421 33.17345728 22.93592976
49.53806482 51.42834925 27.47667578 42.63287002 51.83598398 41.74201585
64.29105027 45.4442762 48.14203525 32.23068171 38.65879878 42.1589835
22.22385827 43.03294579 69.35705425 50.53369246 28.8395517 31.46982728
40.82620585 23.10933924 44.29349148 22.35770791 24.71567401 23.76068779
31.438006 48.99685548 61.2045399 38.36728536 39.68694651 20.22088642
45.70405057 33.47772019 30.57979549 41.00209765 22.23479708 22.70123917
40.5991404 46.02287592 21.23456617 42.76595624 44.74088302 57.87875277
55.99092911 20.91427423 22.43606608 37.71353995 34.24647274 64.55740112
42.21355492 49.77428244 45.32864348 50.27227157 55.69934166 35.90206993
25.49431147 40.39989259 33.55448403 26.10625393 25.78878967 47.13899442
27.84812126 40.79312154 63.42135415 35.40284322 64.36217696 55.09958048
57.11175685 20.55803024 35.16785565 39.51823699 29.52655691 50.90158299
53.83786147 26.02109262 44.8222498 29.21986675 49.01900999 38.28632918
25.06738532 32.8714111 20.79151355 37.84284639 42.83116468 25.12963739
77.84357408 68.14852029 65.30211054 56.23582092 69.28386431 63.75322651]
<class 'numpy.ndarray'>
float64
throat.direct_length
[34.92849839 35.21363372 28.19574436 37.48332963 40.03748244 26.03843313
31.78049716 25.13961018 30.62678566 22.11334439 25.13961018 33.07567082
27. 35.51056181 23.85372088 25.72936066 37.30951621 31.27299154
35.02855978 32.37282811 25.63201124 32.86335345 23.70653918 22.56102835
28.63564213 25.90366769 22.22611077 35.70714214 34.55430509 25.84569597
23.8117618 23.43074903 37.36308338 21.86321111 21.63330765 36.44173432
41.1339276 33.85262176 22.627417 35.73513677 30.43024811 38.26225294
26.92582404 32.87856445 37.16180835 31.30495168 22.47220505 28.42534081
37.88139385 27.83882181 51.38093031 36.23534186 36.29049462 25.90366769
28.21347196 26.21068484 32.03123476 28.87905816 24.12467616 23.15167381
31. 23.40939982 22.18107301 28.12472222 29.76575213 29.83286778
32.17141588 30.14962686 22.56102835 25.41653005 22.91287847 27.89265136
22.82542442 28.77498914 23.36664289 28.28427125 30.77336511 23.10844002
30.77336511 21.84032967 41.01219331 27.11088342 27.25802634 22.97825059
22.737634 24.10394159 23.06512519 31.68595904 36.45545227 35.48239
28.65309756 29.59729717 26.32489316 24.49489743 38.47076812 31.78049716
33.58571125 24.2693222 27.44084547 38.63935817 44.50842617 33.19638535
29. 25.63201124 32.96968304 26.34387974 23.85372088 30.82207001
24.79919354 31.90611227 23.06512519 28.91366459 23.3023604 28.0713377
30.8058436 25.15949125 39.23009049 26.57066051 33.28663395 25.61249695
31.01612484 25.13961018 24.43358345 32.77193922 45.06661736 23.93741841
23.87467277 25.15949125 23.57965225 32.61901286 29.42787794 29.22327839
31.95309062 37.97367509 24.79919354 30.52867504 27.25802634 36.02776707
36.70149861 27.82085549 22.44994432 29.71531592 34.19064199 28.67054237
26.43860813 23.47338919 27.5680975 24.93992783 29.49576241 27.23967694
38.88444419 28.75760769 29.10326442 28.89636655 41.71330723 40.22437072
31.65438358 37.62977544 24.59674775 28. 48.07286137 35.05709629
21.72556098 32.72613634 32.75667871 26.41968963 20.97617696 29.83286778
23.83275058 31.55946768 25.15949125 32. 23.85372088 40.06245125
50.40833264 45.82575695 35.55277767 33.73425559 22.95648057 32.80243893
31.27299154 46.10856753 27.73084925 46.31414471 27.92848009 29.93325909
28.19574436 25.01999201 23.85372088 23.51595203 25.33771892 34.36568055
31.01612484 24.24871131 28.28427125 35.55277767 28.67054237 45.98912915
26.15339366 40.5092582 28.10693865 35.91656999 25.57342371 25.45584412
28.86173938 25.37715508 36.0970913 29.44486373 38.41874542 28.82707061
23.19482701 26.2488095 31.19294792 25.35744467 24.2899156 26.70205985
22.6715681 24.73863375 24.0208243 22.64950331 22.49444376 23.10844002
39.08964057 33.98529094 31.82766093 27.78488798 27.45906044 23.83275058
27.54995463 26.98147513 31. 34.43835072 27.91057147 34.0147027
21.84032967 42.87190222 22.737634 21.84032967 32.37282811 36.26292873
28.05352028 25.63201124 29.54657341 35.7211422 29.41088234 22.04540769
22.09072203 22.42766149 33.21144381 37.30951621 27.16615541 22.86919325
30.4466747 24.22808288 24.79919354 24.59674775 32.80243893 24.14539294
23.4520788 22.53885534 36.72873534 37.06750599 40.9756025 37.36308338
28.77498914 35.70714214 22.49444376 22.4053565 25.35744467 23.40939982
35.29872519 26.73948391 26.15339366 30.06659276 22.04540769 27.94637722
23.23790008 29.3257566 29.51270913 31.85906464 30.06659276 33.52610923
38.27531842 32.21800739 28.3019434 44.31703961 36.81032464 35.36947837
30.59411708 44.65422712 34.19064199 30.65941943 36.08323711 22.71563338
34.53983208 25.74878638 24.43358345 25.78759392 41.01219331 22.627417
29.42787794 32.92415527 35.63705936 28.74021573 30.2654919 35.55277767
22.69361144 26.98147513 22.4053565 22.13594362 41.92851059 32.75667871
31.38470965 32.95451411 37.13488926 43.8178046 35.53871129 26.68332813
24.45403852 21.65640783 27.45906044 27.33130074 28.68797658 28.24889378
39.40812099 36.20773398 28.56571371 25.3179778 23.34523506 34.62657939
35.21363372 43.17406629 34.51086785 23.17326045 22.4053565 43.32435804
18.30300522 38. 26.77685568 34.66987165 28.37252192 38.70400496
36.52396474 34.0147027 38.44476557 29.69848481 36.81032464 43.63484846
70.09992867 46.9041576 37.88139385 47.66550115 44.98888752 34.88552709
53.15072906 39.1535439 75.80237463 54.88169094 44.05678154 46.23851209
60.73713856 39.56008089 62.6019169 67.47592163 41.55718951 37.92097045
44.63182721 34.4818793 37.28270376 43.22036557 40.06245125 43.71498599
37.22902094 42.52058325 43.64630569 32.51153641 28.21347196 32.48076354
27.76688675 26.2488095 37.60319135 36.97296309 26.68332813 39.05124838
41.64132563 41.59326869 30.46309242 31.20897307 38.11823711 40.1248053
51.58488151 43.47413024 54.5802162 34.49637662 22.69361144 27.31300057
58.27520914 32.38826948 45.57411546 39.0256326 42.83689998 36.7559519
31.144823 29.05167809 47.2546294 36.51027253 41.38840417 56.4092191
35.09985755 28.39013913 56.77147171 35.21363372 64.63745044 29.05167809
24.20743687 25.15949125 20.61552813 39.97499218 29.563491 32.60368077
46.27094121 32.69556545 42.53234064 62.86493458 43.43961326 37.68288736
24.91987159 36.66060556 59.49789912 43.84062043 63.65532185 59.66573556
58.13776741 51.41011574 41.52107898 32.10918872 27.73084925 47.57099957
39.56008089 30.56141358 47.92702787 25.25866188 32.58834147 22.93468988
47.20169488 49.1426495 27.4226184 42.10700654 50.18964037 41.55718951
62.72160712 45.43126677 48.12483766 32.15587038 38.62641583 42.14261501
22.18107301 42.3792402 68.12488532 50.5074252 28.80972058 31.32091953
40.63249931 23.06512519 42.68489194 22.22611077 24.59674775 23.72762104
31.17691454 48.97958759 60.25777958 38.34057903 39.33192088 20.174241
43.96589587 33.46640106 30.5450487 40.8900966 22.18107301 22.60530911
40.47221269 45.97825573 21.21320344 41.14608122 44.53088816 56.97367813
55.95533933 20.78460969 22.42766149 37.41657387 33.91164992 64.52131431
42.19004622 49.57822102 44.86646855 49.54795657 54.4334456 35.55277767
25.33771892 37.90778284 33.37663854 26.07680962 25.69046516 47.11687596
27.64054992 39.12799509 63.34824386 35.38361203 64.28841264 55.00909016
56.32938842 20.39607805 35.0142828 39.19183588 29.10326442 47.05316142
45.36518489 25.13961018 43.73785546 29.03446228 49. 38.26225294
24.12467616 32.61901286 20.76053949 35.98610843 41.74925149 24.71841419
71.19691005 61.01639124 58.74521257 53.79591063 66.52067348 60.47313453]
<class 'numpy.ndarray'>
float64
throat.perimeter
[36. 33. 23. 37. 37. 18. 29. 24. 24. 15. 24. 38. 30. 23. 23. 29. 17. 44.
24. 24. 23. 28. 25. 16. 28. 23. 18. 23. 28. 23. 17. 24. 33. 20. 16. 23.
28. 18. 14. 17. 15. 38. 9. 19. 26. 18. 15. 22. 20. 17. 19. 22. 33. 18.
24. 24. 19. 25. 20. 14. 22. 21. 15. 17. 27. 13. 24. 11. 16. 30. 23. 23.
26. 24. 17. 25. 34. 20. 20. 18. 26. 17. 19. 15. 15. 25. 13. 19. 35. 23.
10. 20. 23. 16. 21. 8. 22. 17. 24. 20. 16. 21. 21. 14. 22. 16. 19. 19.
16. 37. 19. 23. 13. 26. 23. 19. 24. 27. 22. 20. 23. 29. 12. 24. 27. 13.
11. 22. 18. 23. 5. 24. 23. 30. 15. 19. 10. 23. 40. 26. 15. 30. 21. 25.
11. 23. 18. 15. 20. 12. 23. 23. 14. 22. 34. 23. 13. 34. 14. 24. 20. 35.
18. 39. 15. 20. 21. 21. 15. 23. 33. 20. 16. 27. 19. 25. 21. 23. 21. 16.
32. 27. 17. 17. 11. 20. 29. 10. 19. 22. 12. 37. 21. 17. 17. 13. 12. 24.
18. 25. 23. 34. 24. 11. 27. 13. 32. 20. 38. 29. 14. 11. 22. 11. 19. 26.
14. 23. 15. 18. 24. 12. 31. 33. 28. 19. 14. 18. 11. 18. 12. 33. 13. 26.
20. 25. 21. 19. 27. 19. 11. 17. 16. 29. 23. 15. 19. 14. 21. 29. 23. 14.
7. 19. 23. 14. 30. 25. 12. 18. 26. 36. 22. 24. 19. 27. 24. 14. 31. 23.
28. 14. 20. 30. 19. 26. 17. 7. 20. 3. 31. 37. 24. 12. 14. 21. 22. 23.
31. 26. 18. 17. 24. 21. 24. 23. 20. 9. 23. 21. 19. 26. 28. 21. 17. 11.
23. 21. 23. 14. 26. 31. 35. 28. 24. 26. 14. 15. 22. 18. 37. 20. 11. 18.
24. 19. 33. 23. 36. 26. 8. 32. 26. 24. 13. 32. 23. 18. 18. 33. 23. 17.
9. 10. 32. 24. 1. 1. 1. 3. 2. 1. 2. 2. 1. 2. 1. 2. 3. 2.
1. 2. 2. 2. 1. 2. 1. 2. 2. 3. 2. 2. 2. 2. 1. 2. 2. 1.
3. 2. 2. 2. 3. 2. 2. 3. 2. 2. 2. 2. 2. 3. 2. 2. 2. 2.
1. 2. 1. 2. 2. 2. 2. 3. 2. 3. 2. 3. 2. 2. 2. 2. 1. 2.
2. 3. 3. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 3. 3. 2. 2. 2.
3. 2. 2. 2. 2. 2. 2. 2. 2. 2. 3. 2. 1. 2. 2. 2. 1. 2.
2. 3. 2. 2. 2. 2. 2. 3. 3. 2. 3. 2. 3. 2. 1. 2. 3. 2.
2. 2. 2. 2. 2. 2. 1. 2. 2. 2. 2. 2. 2. 3. 2. 1. 2. 3.
3. 2. 2. 2. 3. 3. 2. 2. 3. 3. 2. 2. 3. 1. 2. 2. 3. 3.
2. 1. 2. 2. 3. 2. 2. 3. 2. 2. 2. 3. 1. 3. 2. 2. 2. 3.
2. 2. 2. 1. 2. 2. 1. 1. 1. 1. 1. 1.]
<class 'numpy.ndarray'>
float64
pore.volume
[ 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793. 793.
793. 793. 793. 793. 793. 793. 793. 793. 793. 542. 1619. 1180.
560. 2165. 2762. 1624. 495. 948. 668. 373. 254. 684. 1336. 412.
298. 1072. 245. 1185. 656. 1649. 2067. 548. 544. 402. 1346. 447.
856. 273. 577. 1011. 965. 757. 1617. 304. 330. 297. 430. 831.
1010. 1016. 486. 463. 294. 2124. 2968. 1700. 1130. 457. 316. 984.
716. 473. 294. 489. 729. 2570. 1027. 355. 2316. 1285. 406. 354.
488. 384. 617. 2158. 449. 387. 788. 350. 260. 272. 374. 269.
1447. 373. 589. 258. 1479. 595. 2225. 261. 366. 935. 573. 362.
304. 1968. 1536. 466. 1374. 568. 599. 520. 1770. 796. 731. 285.
232. 707. 2512. 1817. 1290. 1614. 1371. 142. 615.]
<class 'numpy.ndarray'>
float64
pore.surface_area
[ -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4.
-4. -4. -4. -4. -4. -4. -4. -4. -4. -4. -4. 75. 164. 144.
90. 202. 195. 119. 90. 94. 101. 71. 57. 87. 127. 80. 57. 100.
47. 98. 102. 113. 177. 77. 69. 86. 109. 79. 111. 54. 79. 113.
104. 91. 176. 56. 52. 56. 62. 89. 101. 107. 68. 69. 60. 154.
211. 121. 92. 82. 60. 96. 103. 79. 62. 86. 80. 210. 100. 59.
158. 105. 63. 80. 50. 66. 87. 158. 80. 84. 104. 67. 57. 46.
67. 74. 150. 57. 46. 56. 141. 81. 168. 52. 87. 95. 66. 62.
87. 149. 147. 54. 99. 98. 66. 89. 127. 83. 71. 79. 54. 71.
183. 175. 179. 162. 157. 57. 124.]
<class 'numpy.ndarray'>
float64
throat.cross_sectional_area
[36. 33. 23. 37. 37. 18. 29. 24. 24. 15. 24. 38. 30. 23. 23. 29. 17. 44.
24. 24. 23. 28. 25. 16. 28. 23. 18. 23. 28. 23. 17. 24. 33. 20. 16. 23.
28. 18. 14. 17. 15. 38. 9. 19. 26. 18. 15. 22. 20. 17. 19. 22. 33. 18.
24. 24. 19. 25. 20. 14. 22. 21. 15. 17. 27. 13. 24. 11. 16. 30. 23. 23.
26. 24. 17. 25. 34. 20. 20. 18. 26. 17. 19. 15. 15. 25. 13. 19. 35. 23.
10. 20. 23. 16. 21. 8. 22. 17. 24. 20. 16. 21. 21. 14. 22. 16. 19. 19.
16. 37. 19. 23. 13. 26. 23. 19. 24. 27. 22. 20. 23. 29. 12. 24. 27. 13.
11. 22. 18. 23. 5. 24. 23. 30. 15. 19. 10. 23. 40. 26. 15. 30. 21. 25.
11. 23. 18. 15. 20. 12. 23. 23. 14. 22. 34. 23. 13. 34. 14. 24. 20. 35.
18. 39. 15. 20. 21. 21. 15. 23. 33. 20. 16. 27. 19. 25. 21. 23. 21. 16.
32. 27. 17. 17. 11. 20. 29. 10. 19. 22. 12. 37. 21. 17. 17. 13. 12. 24.
18. 25. 23. 34. 24. 11. 27. 13. 32. 20. 38. 29. 14. 11. 22. 11. 19. 26.
14. 23. 15. 18. 24. 12. 31. 33. 28. 19. 14. 18. 11. 18. 12. 33. 13. 26.
20. 25. 21. 19. 27. 19. 11. 17. 16. 29. 23. 15. 19. 14. 21. 29. 23. 14.
7. 19. 23. 14. 30. 25. 12. 18. 26. 36. 22. 24. 19. 27. 24. 14. 31. 23.
28. 14. 20. 30. 19. 26. 17. 7. 20. 3. 31. 37. 24. 12. 14. 21. 22. 23.
31. 26. 18. 17. 24. 21. 24. 23. 20. 9. 23. 21. 19. 26. 28. 21. 17. 11.
23. 21. 23. 14. 26. 31. 35. 28. 24. 26. 14. 15. 22. 18. 37. 20. 11. 18.
24. 19. 33. 23. 36. 26. 8. 32. 26. 24. 13. 32. 23. 18. 18. 33. 23. 17.
9. 10. 32. 24. 22. 4. 1. 8. 8. 10. 4. 6. 10. 6. 1. 5. 9. 6.
19. 19. 6. 13. 18. 28. 5. 8. 27. 7. 3. 7. 5. 10. 17. 20. 6. 9.
11. 25. 16. 5. 7. 35. 12. 5. 7. 28. 12. 7. 6. 7. 7. 13. 17. 6.
3. 20. 20. 7. 7. 7. 10. 9. 4. 10. 17. 6. 6. 15. 6. 11. 1. 14.
9. 11. 11. 15. 16. 8. 7. 13. 14. 4. 18. 15. 15. 7. 26. 7. 9. 11.
15. 8. 12. 29. 22. 6. 18. 3. 7. 24. 14. 15. 3. 6. 6. 22. 1. 23.
5. 10. 4. 13. 7. 9. 12. 23. 8. 17. 23. 16. 16. 12. 1. 21. 15. 8.
11. 11. 6. 24. 5. 15. 2. 6. 9. 5. 7. 11. 6. 6. 9. 1. 6. 5.
5. 15. 24. 23. 6. 6. 7. 15. 9. 25. 8. 6. 6. 7. 10. 27. 15. 12.
10. 2. 5. 23. 9. 14. 10. 25. 9. 10. 32. 10. 9. 20. 11. 4. 10. 32.
21. 27. 9. 1. 5. 23. 16. 25. 23. 5. 2. 4.]
<class 'numpy.ndarray'>
float64
throat.equivalent_diameter
[6.770275 6.48204481 5.41151638 6.86366252 6.86366252 4.78730736
6.07650778 5.52790639 5.52790639 4.37019372 5.52790639 6.95579634
6.18038723 5.41151638 5.41151638 6.07650778 4.65242649 7.48482064
5.52790639 5.52790639 5.41151638 5.97082132 5.64189584 4.51351667
5.97082132 5.41151638 4.78730736 5.41151638 5.97082132 5.41151638
4.65242649 5.52790639 6.48204481 5.04626504 4.51351667 5.41151638
5.97082132 4.78730736 4.22200825 4.65242649 4.37019372 6.95579634
3.3851375 4.91849076 5.75362739 4.78730736 4.37019372 5.29256743
5.04626504 4.65242649 4.91849076 5.29256743 6.48204481 4.78730736
5.52790639 5.52790639 4.91849076 5.64189584 5.04626504 4.22200825
5.29256743 5.17088295 4.37019372 4.65242649 5.86323014 4.06842895
5.52790639 3.74241032 4.51351667 6.18038723 5.41151638 5.41151638
5.75362739 5.52790639 4.65242649 5.64189584 6.57952464 5.04626504
5.04626504 4.78730736 5.75362739 4.65242649 4.91849076 4.37019372
4.37019372 5.64189584 4.06842895 4.91849076 6.67558118 5.41151638
3.56824823 5.04626504 5.41151638 4.51351667 5.17088295 3.19153824
5.29256743 4.65242649 5.52790639 5.04626504 4.51351667 5.17088295
5.17088295 4.22200825 5.29256743 4.51351667 4.91849076 4.91849076
4.51351667 6.86366252 4.91849076 5.41151638 4.06842895 5.75362739
5.41151638 4.91849076 5.52790639 5.86323014 5.29256743 5.04626504
5.41151638 6.07650778 3.9088201 5.52790639 5.86323014 4.06842895
3.74241032 5.29256743 4.78730736 5.41151638 2.52313252 5.52790639
5.41151638 6.18038723 4.37019372 4.91849076 3.56824823 5.41151638
7.13649646 5.75362739 4.37019372 6.18038723 5.17088295 5.64189584
3.74241032 5.41151638 4.78730736 4.37019372 5.04626504 3.9088201
5.41151638 5.41151638 4.22200825 5.29256743 6.57952464 5.41151638
4.06842895 6.57952464 4.22200825 5.52790639 5.04626504 6.67558118
4.78730736 7.04672564 4.37019372 5.04626504 5.17088295 5.17088295
4.37019372 5.41151638 6.48204481 5.04626504 4.51351667 5.86323014
4.91849076 5.64189584 5.17088295 5.41151638 5.17088295 4.51351667
6.38307649 5.86323014 4.65242649 4.65242649 3.74241032 5.04626504
6.07650778 3.56824823 4.91849076 5.29256743 3.9088201 6.86366252
5.17088295 4.65242649 4.65242649 4.06842895 3.9088201 5.52790639
4.78730736 5.64189584 5.41151638 6.57952464 5.52790639 3.74241032
5.86323014 4.06842895 6.38307649 5.04626504 6.95579634 6.07650778
4.22200825 3.74241032 5.29256743 3.74241032 4.91849076 5.75362739
4.22200825 5.41151638 4.37019372 4.78730736 5.52790639 3.9088201
6.28254931 6.48204481 5.97082132 4.91849076 4.22200825 4.78730736
3.74241032 4.78730736 3.9088201 6.48204481 4.06842895 5.75362739
5.04626504 5.64189584 5.17088295 4.91849076 5.86323014 4.91849076
3.74241032 4.65242649 4.51351667 6.07650778 5.41151638 4.37019372
4.91849076 4.22200825 5.17088295 6.07650778 5.41151638 4.22200825
2.98541066 4.91849076 5.41151638 4.22200825 6.18038723 5.64189584
3.9088201 4.78730736 5.75362739 6.770275 5.29256743 5.52790639
4.91849076 5.86323014 5.52790639 4.22200825 6.28254931 5.41151638
5.97082132 4.22200825 5.04626504 6.18038723 4.91849076 5.75362739
4.65242649 2.98541066 5.04626504 1.95441005 6.28254931 6.86366252
5.52790639 3.9088201 4.22200825 5.17088295 5.29256743 5.41151638
6.28254931 5.75362739 4.78730736 4.65242649 5.52790639 5.17088295
5.52790639 5.41151638 5.04626504 3.3851375 5.41151638 5.17088295
4.91849076 5.75362739 5.97082132 5.17088295 4.65242649 3.74241032
5.41151638 5.17088295 5.41151638 4.22200825 5.75362739 6.28254931
6.67558118 5.97082132 5.52790639 5.75362739 4.22200825 4.37019372
5.29256743 4.78730736 6.86366252 5.04626504 3.74241032 4.78730736
5.52790639 4.91849076 6.48204481 5.41151638 6.770275 5.75362739
3.19153824 6.38307649 5.75362739 5.52790639 4.06842895 6.38307649
5.41151638 4.78730736 4.78730736 6.48204481 5.41151638 4.65242649
3.3851375 3.56824823 6.38307649 5.52790639 5.29256743 2.25675833
1.12837917 3.19153824 3.19153824 3.56824823 2.25675833 2.7639532
3.56824823 2.7639532 1.12837917 2.52313252 3.3851375 2.7639532
4.91849076 4.91849076 2.7639532 4.06842895 4.78730736 5.97082132
2.52313252 3.19153824 5.86323014 2.98541066 1.95441005 2.98541066
2.52313252 3.56824823 4.65242649 5.04626504 2.7639532 3.3851375
3.74241032 5.64189584 4.51351667 2.52313252 2.98541066 6.67558118
3.9088201 2.52313252 2.98541066 5.97082132 3.9088201 2.98541066
2.7639532 2.98541066 2.98541066 4.06842895 4.65242649 2.7639532
1.95441005 5.04626504 5.04626504 2.98541066 2.98541066 2.98541066
3.56824823 3.3851375 2.25675833 3.56824823 4.65242649 2.7639532
2.7639532 4.37019372 2.7639532 3.74241032 1.12837917 4.22200825
3.3851375 3.74241032 3.74241032 4.37019372 4.51351667 3.19153824
2.98541066 4.06842895 4.22200825 2.25675833 4.78730736 4.37019372
4.37019372 2.98541066 5.75362739 2.98541066 3.3851375 3.74241032
4.37019372 3.19153824 3.9088201 6.07650778 5.29256743 2.7639532
4.78730736 1.95441005 2.98541066 5.52790639 4.22200825 4.37019372
1.95441005 2.7639532 2.7639532 5.29256743 1.12837917 5.41151638
2.52313252 3.56824823 2.25675833 4.06842895 2.98541066 3.3851375
3.9088201 5.41151638 3.19153824 4.65242649 5.41151638 4.51351667
4.51351667 3.9088201 1.12837917 5.17088295 4.37019372 3.19153824
3.74241032 3.74241032 2.7639532 5.52790639 2.52313252 4.37019372
1.59576912 2.7639532 3.3851375 2.52313252 2.98541066 3.74241032
2.7639532 2.7639532 3.3851375 1.12837917 2.7639532 2.52313252
2.52313252 4.37019372 5.52790639 5.41151638 2.7639532 2.7639532
2.98541066 4.37019372 3.3851375 5.64189584 3.19153824 2.7639532
2.7639532 2.98541066 3.56824823 5.86323014 4.37019372 3.9088201
3.56824823 1.59576912 2.52313252 5.41151638 3.3851375 4.22200825
3.56824823 5.64189584 3.3851375 3.56824823 6.38307649 3.56824823
3.3851375 5.04626504 3.74241032 2.25675833 3.56824823 6.38307649
5.17088295 5.86323014 3.3851375 1.12837917 2.52313252 5.41151638
4.51351667 5.64189584 5.41151638 2.52313252 1.59576912 2.25675833]
<class 'numpy.ndarray'>
float64
══════════════════════════════════════════════════════════════════════════════
net : <openpnm.network.Network at 0x18f49bbb070>
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
# Properties Valid Values
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
2 throat.conns 534 / 534
3 pore.coords 189 / 189
4 pore.region_label 189 / 189
5 pore.phase 189 / 189
6 throat.phases 534 / 534
7 pore.region_volume 189 / 189
8 pore.equivalent_diameter 189 / 189
9 pore.local_peak 189 / 189
10 pore.global_peak 189 / 189
11 pore.geometric_centroid 189 / 189
12 throat.global_peak 534 / 534
13 pore.inscribed_diameter 189 / 189
14 pore.extended_diameter 189 / 189
15 throat.inscribed_diameter 534 / 534
16 throat.total_length 534 / 534
17 throat.direct_length 534 / 534
18 throat.perimeter 534 / 534
19 pore.volume 189 / 189
20 pore.surface_area 189 / 189
21 throat.cross_sectional_area 534 / 534
22 throat.equivalent_diameter 534 / 534
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
# Labels Assigned Locations
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
2 pore.all 189
3 throat.all 534
4 pore.solid 81
5 throat.solid_void 346
6 pore.void 108
7 throat.void_solid 346
8 throat.void_void 188
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Now we can see that the phases are named using our preferred nomenclature of “solid” and “void”. This is helpful if you have several phases like “electrolyte”, “binder”, “particles” for instance.
boundary_width#
Adding pores (or more generally nodes) on the boundaries of images is helpful when conducting transport simulations. Without boundary pores then boundary condtions must be applied to internal pores which are (a) hard to identify clearly and (b) make it impossible to know the exact length of the domain.
Note that boundary nodes are not physical and thus their sizes are ficticious. This can cause problems when computing the transport conductance for these nodes, so care must be taken.
The boundary_width argument was designed to work analogously to the numpy.pad function. You can specify different paddings along each axis and also along each face. For instance, here are some options (for a 2D image):
[0, 3]: 3 voxels only applied to the y-axis.[0, [0, 3]]: 3 voxels only applied to the end of y-axis.[0, [3, 0]]: 3 voxels only applied to the beginning of y-axis.
im = ps.generators.blobs([400, 400], porosity=0.6)
a = ps.networks.snow2(im, boundary_width=[[5, 0], 10])
fig, ax = plt.subplots(figsize=[6, 6])
ax.imshow(a.regions, origin='lower', interpolation='none')
ax.axis(False);
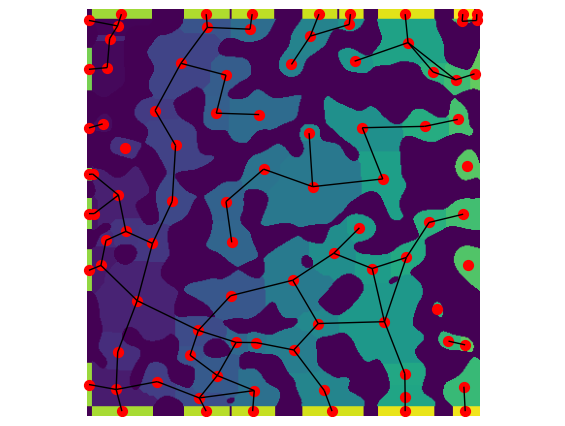
A few things to note:
The image contains regions on the left, right and bottom faces, which are added by padding the image after the segmentation was applied, then incrementing labels the padded regions so their labels are greater than any inside the original image.
These new regions are then treated like a normal region when the network topology and geometry is extracted.
The width of each boundary region is nearly the same as the corresponding internal regions, but they are only a few voxels thick (in this case because we specified 5 or 10). This means that the value of ‘pore.inscribed’ sphere for this regions will almost all be 5 or 10 voxels.
The solid touching the boundaries creates gaps in the boundary regions.
Two boundary regions neighboring each other are separated by 2 voxels. This prevents them from being considered as connected during the topology extraction stage.
The top and bottom of the image do not have any boundaries because we set the widths to 0 on this axis.
It is instructive to visualize the network over the image to see how the boundary pores work:
pn = op.io.network_from_porespy(a.network)
ax = op.visualization.plot_connections(pn, c='k')
ax = op.visualization.plot_coordinates(pn, markersize=50, ax=ax)
fig, ax = plt.gcf(), plt.gca()
ax.imshow(a.regions.T)
ax.axis(False);
accuracy#
This argument can either take the value of 'high' or 'standard', with standard being the default. It is not recommended to use 'high' since this uses some rather slow functions to measure the surface areas and perimeters. The increase in accuracy is basically futile since (a) the image has already been reduced to a coarse voxelization and (b) the pore network abstraction discards information about the actual microstructure in exchange for speed, so spending ages on the extraction step would undermine this purpose.
voxel_size#
This is the voxel size of the image, as in the length of one side of a voxel. Typical microtomography images are in the range of 1-5 um per voxel. NanoCT can be as low as 16 nm per voxel. FIB-SEM might be 4 nm per voxel. Note that all properties returned from the snow2 function, like ‘pore.volume’ will be in the same units are this value. It is strongly recommended to use SI, which is assumed in OpenPNM for most of the fluid property calculations.
sigma and r_max#
These values are passed on to the gaussian_blur and find_peaks functions.
The gaussian_blur is applied to the distance transfrom, which as discussed in the original snow paper is a very effective way to reduce the number of incorrect peaks that are found in the subsequent steps. A value of sigma=0.4 is the default.
The find_peaks function applies a maximum filter to the distance transform, which replaces each voxel with the maximum it finds with the specified neighborhood. It then looks for voxels that are the same between the filtered image and the original distance transform. Only voxels that are local maximas will be the same between the images.
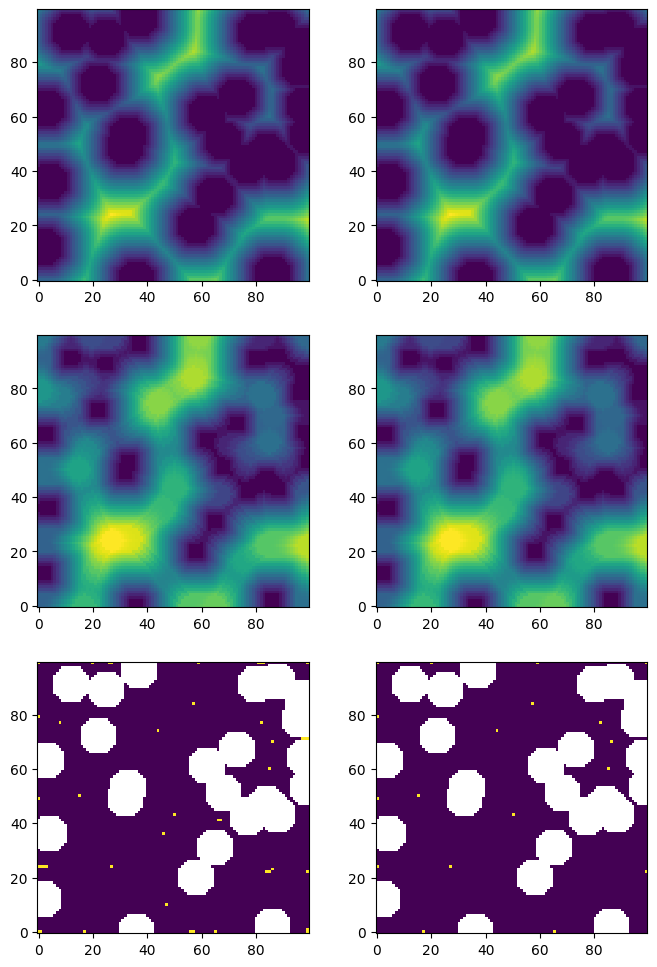
The following code block illustrates the impact of applying the gaussian_blur filter on finding peaks.
np.random.seed(13)
im = ps.generators.overlapping_spheres([100, 100], r=7, porosity=0.7)
dt = edt(im)
mx1 = spim.maximum_filter(dt, footprint=ps.tools.ps_disk(r=4, smooth=False))
pk1 = dt == mx1
dt_blur = spim.gaussian_filter(dt, sigma=0.4)
mx2 = spim.maximum_filter(dt_blur, footprint=ps.tools.ps_disk(r=4, smooth=False))
pk2 = dt_blur == mx2
fig, ax = plt.subplots(3, 2, figsize=[8, 12])
ax[0][0].imshow(dt, origin='lower', interpolation='none')
ax[1][0].imshow(mx1, origin='lower', interpolation='none')
ax[2][0].imshow(pk1/im, origin='lower', interpolation='none')
ax[0][1].imshow(dt_blur, origin='lower', interpolation='none')
ax[1][1].imshow(mx2, origin='lower', interpolation='none')
ax[2][1].imshow(pk2/im, origin='lower', interpolation='none');
peaks#
Because finding correct peaks is such an important part marker-based watershed segmentationa, and therefore of snow2, it is possible to supply custom peaks found using any desired process. Obviously, if this is provided then sigma and r_max are ignored.
Let’s use the two sets of peaks found above:
net1 = ps.networks.snow2(phases=im, boundary_width=0, peaks=pk1)
net2 = ps.networks.snow2(phases=im, boundary_width=0, peaks=pk2)
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
ax[0].imshow(net1.regions, origin='lower', interpolation='none')
ax[1].imshow(net2.regions, origin='lower', interpolation='none')
ax[0].axis(False)
ax[1].axis(False);
Clearly the image on the left is ‘over segmented’ while the image on the right seems to have identified the pores nearly perfectly, even without subsequent processing of the peaks that normally occur in snow2 like trim_saddle_points and trim_nearby_peaks.
parallelization#
The watershed function was identified as the bottleneck of the entire process, especially as images grew in size. Parallelization of the watershed function had not be throughly investigated in the literature, so Khan et al developed a basic protocol for dividing the image into chunks and processing each in parallel. The main challenge with this approach was ensuring sufficient overlap was allowed to prevent any artifacts, while not being overly conservative since large overlaps undermine the speedup obtained by parallelization. The parallelization if accomplished by dask which makes it trivial to dispatch duplicate jobs to different cores.
The snow2 function can optionally parallelize the watershed step. It calls porespy.filters.snow_partitioning_parallel behind the scenes, but this function requires several arguments. Instead of complicating the snow2 function signature, we instead chose to accept a dict of arguments and values which are then passed on. These are:
divs: The number of chunks to divide the image into. A value of 2 means the image is divided in hald along each axis, for a total of 8 chunks in a 3D image. It’s possible to specify a different number of divisions in each direction, likedivs=[2, 2, 1]. This could be useful if the image to be processed is very narrow in one direction, such as a piece of fibrous electrode.overlap: This controls the amount of overlap between each chunk in voxels. SpecifyingNone(the default) means that the algorithm finds the overlap automatically. Khan el al found that using the maximum of the distance tranform was suitable.cores: This controls the number of cores to use when processing the chunks. If not provided then all cores will be used. This may be problematic on computers without a large amount of RAM since each process will consume some RAM. In these cases in may be beneficial to set cores to a small number and simply wait longer for the result.
If parallel_kw=None then no parallelization is applied, while if parallel_kw={} then the default arguments of the snow_partitioning_parallel function are used.
In the following code block, the parallelization option is demonstrated with an overlap that is too small, resulting in a noticable artifacts in the center sectionof the watershed segmentation, where the divsions were located. For comparison, the same image is processed with the default overlap.
np.random.seed(0)
im = ps.generators.overlapping_spheres([400, 400], r=20, porosity=0.8)
parallel_kw = {'cores': 1, 'divs': [2, 2], 'overlap': 1}
net1 = ps.networks.snow2(phases=im, parallel_kw=parallel_kw)
parallel_kw = {'cores': 1, 'divs': [2, 2], 'overlap': None}
net2 = ps.networks.snow2(phases=im, parallel_kw=parallel_kw)
[10:50:17] WARNING Disabling paralelization as overlap exceeds than chunk size. _snow2.py:222
WARNING Disabling paralelization as overlap exceeds than chunk size. _snow2.py:222
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
temp = ps.tools.randomize_colors(net1.regions)
ax[0].imshow(temp, origin='lower', interpolation='none')
ax[0].axis(False)
temp = ps.tools.randomize_colors(net2.regions)
ax[1].imshow(temp, origin='lower', interpolation='none')
ax[1].axis(False);
