norm_to_uniform

Import packages

import numpy as np
import porespy as ps
import scipy.ndimage as spim
import matplotlib.pyplot as plt
import skimage
ps.visualization.set_mpl_style()

[17:45:18] ERROR    PARDISO solver not installed, run `pip install pypardiso`. Otherwise,          _workspace.py:56
                    simulations will be slow. Apple M chips not supported.                                         

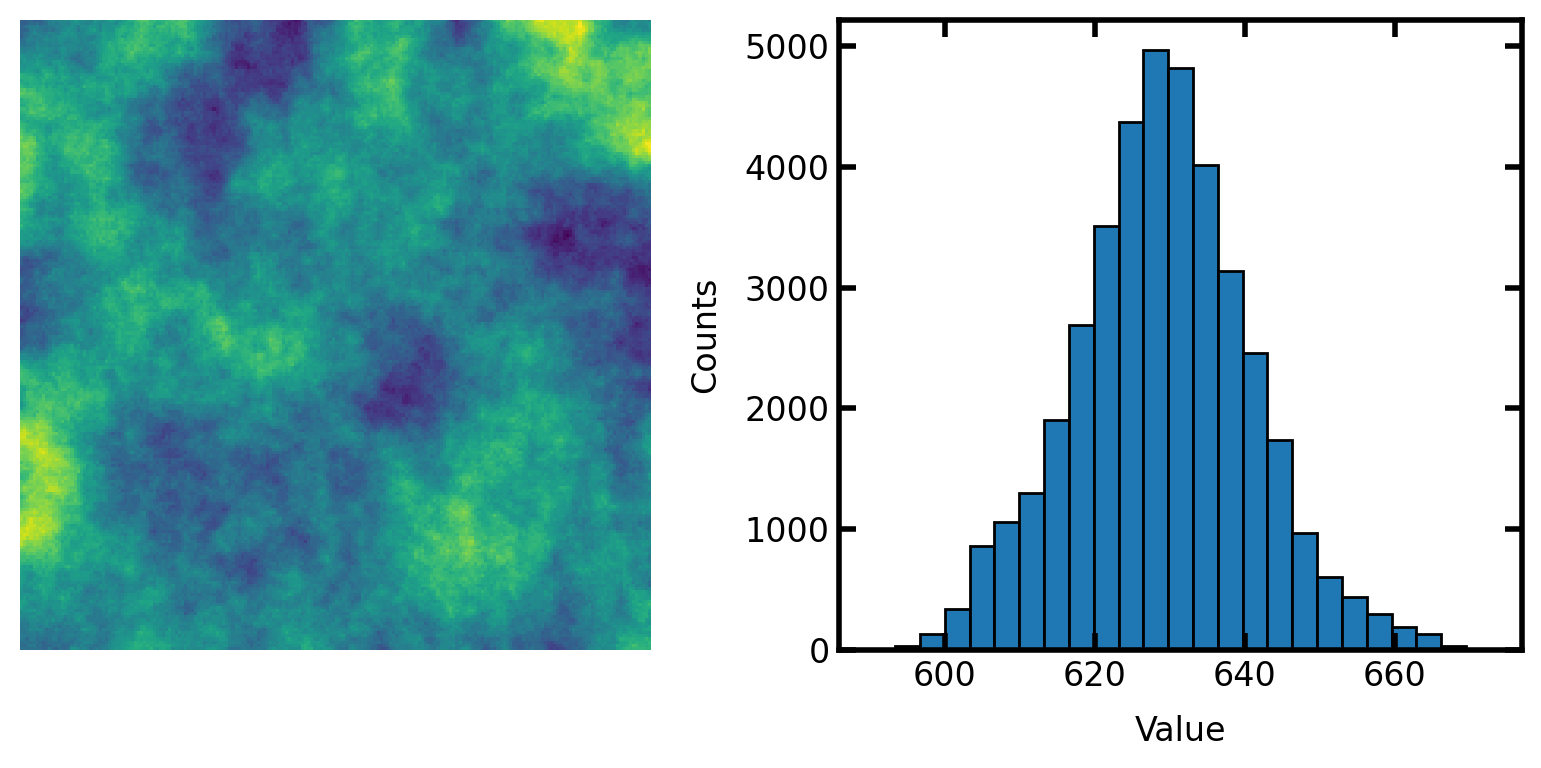
Generate image for testing

im = np.random.rand(200, 200)
strel = ps.tools.ps_disk(20, smooth=False)
im = spim.convolve(im, weights=strel)
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
ax[0].axis(False)
ax[0].imshow(im)
ax[1].hist(im.flatten(), edgecolor='k', bins=25)
ax[1].set_xlabel('Value')
ax[1].set_ylabel('Counts');

Demonstrate function

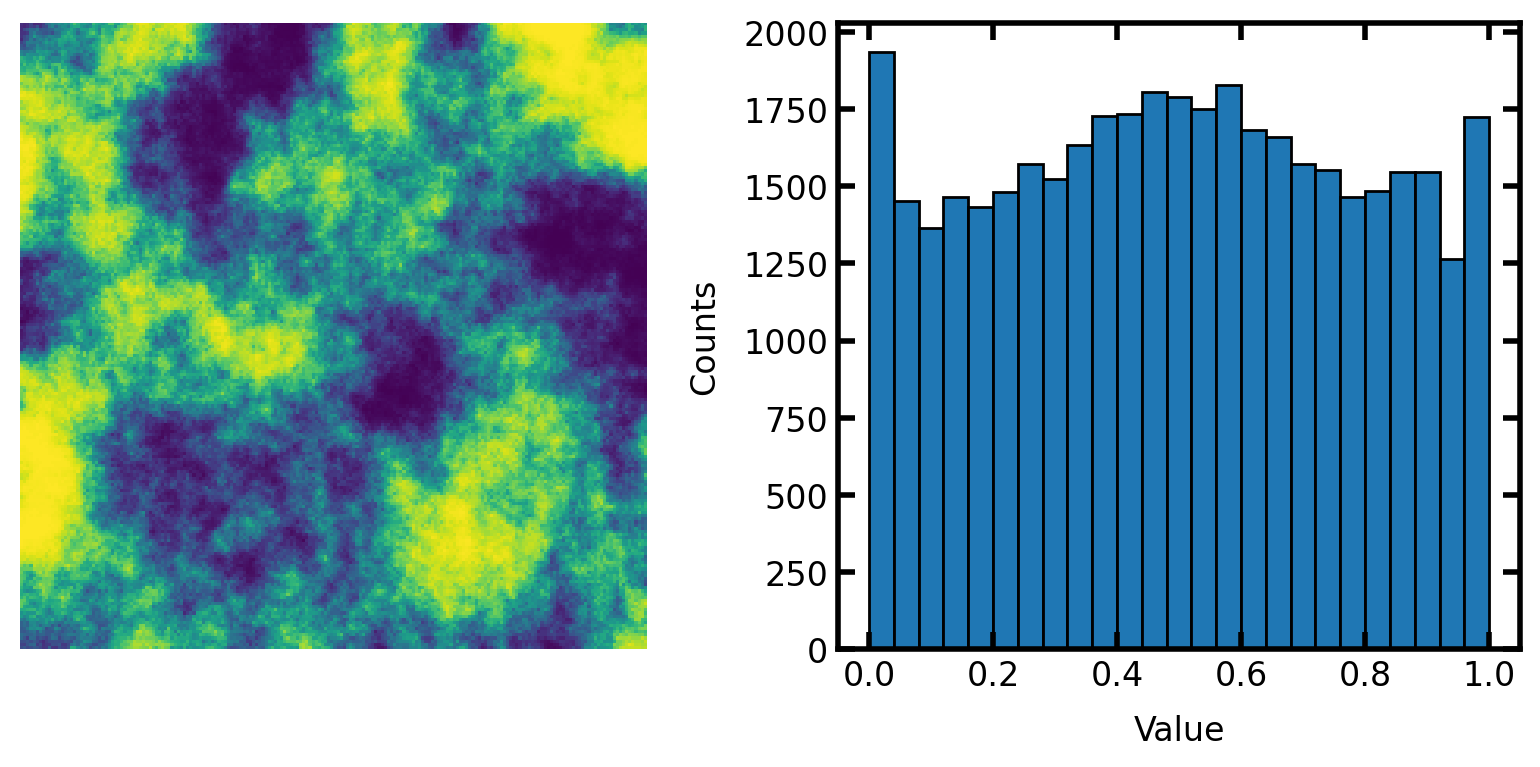
The correlated noise field generated above has approximatetly normally distributed values. It’s not perfectly normal, but it’s pretty close. This can be converted to uniformly distributed values as follows:

im1 = ps.tools.norm_to_uniform(im=im)
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
ax[0].axis(False)
ax[0].imshow(im1)
ax[1].hist(im1.flatten(), edgecolor='k', bins=25)
ax[1].set_xlabel('Value')
ax[1].set_ylabel('Counts');

scale

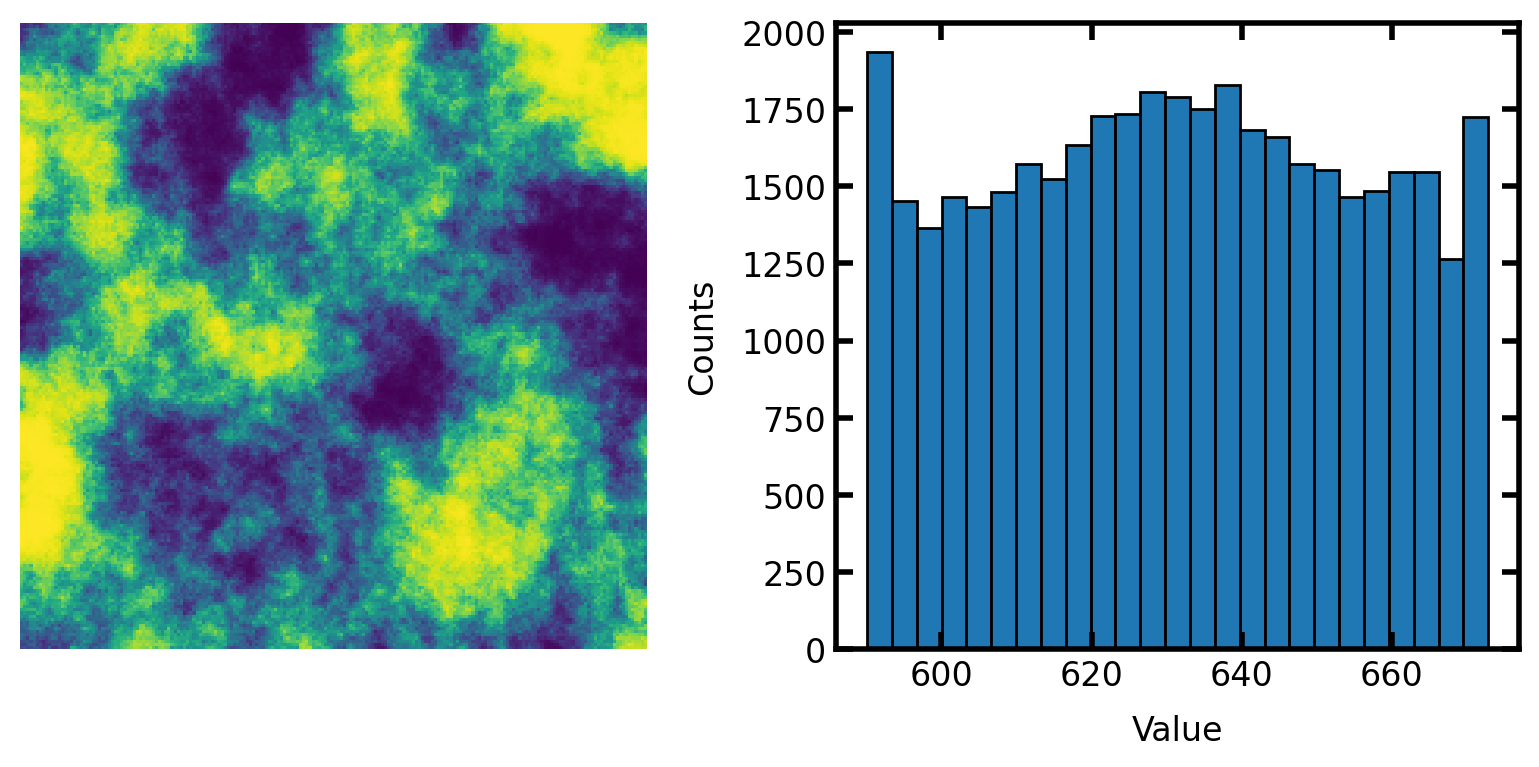
The output can be scale to a specific range:

im2 = ps.tools.norm_to_uniform(im=im, scale=[0, 1])
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
ax[0].axis(False)
ax[0].imshow(im2)
ax[1].hist(im2.flatten(), edgecolor='k', bins=25)
ax[1].set_xlabel('Value')
ax[1].set_ylabel('Counts');